Official LSV Web Site
FAST - Fast Acceleration of Symbolic Transition systems

News
-
NEW (12/04/2006): FAST Extended Release is available.
- The architecture has been re-designed and it is now really easy to plug any Presburger library to FAST.
- The tool package includes pluggings for existing libraries MONA, LASH and OMEGA.
- A new library implementing Shared Automata (automata with computation cache) is provided, but it is still being optimized.
- Finally, the user can now specify circuits of interest to be used in priority and choose between different acceleration algorithms.
- 10/06/2004: lots of goodies (Emacs mod, translator from PNML to FAST, ...)
- 14/08/2003: INTERFAST version 1.0 is available under GPL.
- 31/07/2003: FAST version 1.0 is available under GPL.

Introduction
Model-checking is a wide-spread technique in critical systems verification.
Several efficient model-checkers are
available. However, most of these tools are restricted
to finite systems whereas many real systems are infinite, because of parameters
or unbounded data structures.
FAST is a tool dedicated to the analysis of infinite
systems. It performs automatic verification of systems augmented with
(unbounded)
integer variables. The main issue
addressed by FAST is the computation of the exact (infinite) set of
configurations reachable from a given set of initial configurations. Although
such sets are in general not computable, FAST uses a semi-algorithm
which is expected to terminate in most practical cases.
The techniques used in FAST are based on acceleration, which involves computing the effect of iterating
a control loop of arbitrary length. FAST is also the first tool to use an heuristics to find automatically the good cycles to accelerate (in other accelerated symbolic model-checkers, the user has to provide such cycles). The models FAST operates on are
composed of a finite control structure, guards are Presburger formulae, and
operations affine functions. The user can provide
a strategy to direct the reachability set computation. Strategies are written
in a high-level language, which supports, for the moment, forward and backward
reachability as well as more advanced constructs such as incremental sub-model
analysis.
FAST has been applied to a large number of examples, ranging from tricky academic puzzles to communication protocols or multi-threaded JAVA programs. These examples are available here. In about 80% of these case studies the reachability set could effectively be computed using a forward algorithm and a basic predefined strategy.
More elaborate strategies or a backward algorithm can lead to a
considerable drop in computation time for some protocols.
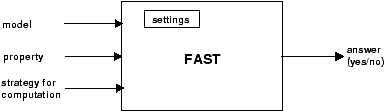
FAST inputs and outputs.

Comparison with other tools
Other tools exist for the verification of unbounded counter automata. The following table shows a comparison between FAST and some of these tools. The main advantages of FAST are that FAST:- has a powerful model which allows to express easily most systems,
- uses acceleration and heuristics to compute automatically the reachability set in most practical cases,
- is user-friendly thanks to its GUI (InterFAST).

References
FAST
- S. Bardin, J. Leroux, and G. Point. FAST Extended Release . In Proc. 18th Conf. Computer Aided Verification (CAV'2006), Seattle,Washington,USA, August 2006, Lecture Notes in Computer Science. Springer, 2006. To appear.
- S. Bardin, A. Finkel, J. Leroux, and L. Petrucci. FAST: Fast Accelereation of Symbolic Transition systems . In Proc. 15th Conf. Computer Aided Verification (CAV'2003), Boulder,CO,USA, July 2003, volume 2725 of Lecture Notes in Computer Science. Springer, 2003.
- S. Bardin, A. Finkel, J. Leroux, L. Petrucci and L. Worobel. FAST Users' Manual. (14 august 2003)
- S. Bardin and L. Petrucci. From PNML to counter systems for accelerating Petri Nets with FAST . In Proc. Workshop on Interchange Format for Petri Nets, Bologna,Italy, June 2004, to appear.
Acceleration
- S. Bardin, A. Finkel, and J. Leroux. FASTer acceleration of counter automata in practice . In Proc. 10th Int. Conf. Tools and Algorithms for the Construction and Analysis of Systems (TACAS'2004), Barcelona, Spain,, April 2004, volume 2988 of Lecture Notes in Computer Science, pages 576-590. Springer, 2004.
- A. Finkel and J. Leroux. How to compose Presburger-accelerations: Applications to broadcast protocols. In Proc. 22nd Conf. Found. of Software Technology and Theor. Comp. Sci. (FST&TCS'2002), Kanpur, India, Dec. 2002, volume 2556 of Lecture Notes in Computer Science, pages 145-156. Springer, 2002.
Flattable systems
- S. Bardin, A. Finkel, J. Leroux and P. Schnoebelen. Flat acceleration in symbolic model checking. In Proc. of the 3rd International Symposium on Automated Technology for Verification and Analysis (ATVA'05), Springer, 2005.
- J. Leroux and G. Sutre. Flat counter automata almost everywhere! In Proc. of the 3rd International Symposium on Automated Technology for Verification and Analysis (ATVA'05), Springer, 2005.
- J. Leroux and G. Sutre. On flatness for 2-dimensional vector addition systems with states . In Proc. 15th Int. Conf. Concurrency Theory (CONCUR 2004) , volume 3170 of Lecture Notes in Computer Science, pages 402-416. Springer, 2005.
Other
- J. Leroux. A Polynomial Time Presburger Criterion and Synthesis for Number Decision Diagrams. In Proc. 20th IEEE Symp. Logic in Computer Science (LICS 2005) , Chicago, USA, June 2005, IEEE Comp. Soc. Press. 2005.
- Ch. Darlot, A. Finkel and L. Van Begin. About Fast and TReX accelerations. In Proceedings of the 4th International Workshop on Automated Verification of Critical Systems (AVoCS 2004) , London, UK, August-September 2004, ENTCS 128(6), pages 87-103. Elsevier Science Publishers, 2005.

Experiments
- This table shows the time and memory needed for FAST to compute the reachability set of several protocols, using a forward algorithm and a basic strategy. Note that computing the whole reachability set is really harder than just checking on-the-fly if a configuration is reachable using a backward algorithm. Some tools are restricted to the second method, while FAST can perform both. Even if benchmarks for the backward algorithm are not complete (it takes time!!), experimentations show better results using backward algorithm.
- All examples

Installation
- pnml2fst, a translator of Petri Nets described in the standard PNML format into FAST input model
- Emacs mod for FAST
- Binaries of FAST (version 1.0, Linux, processor x86) gcc 3.3.3
- Binaries of InterFAST, GUI for FAST (version 1.0, java)
- Manual for FAST (.ps) (14 august 2003)
- Overview of FAST (.pdf)

FAST team
- Sébastien Bardin at LSV
- Alain Finkel at LSV
- Jérôme Leroux at LSV
- Laure Petrucci at LIPN
Former
- Laurent Worobel (2003)
- Laurent Van Begin (2003)
- Christophe Darlot (2003-2004)