The shrinktech Tool
Example
Non-shrinkability of timed automata can be due either to the disappearance of a finite behaviour, or that of an infinite behaviour. We illustrate the first kind of non-shrinkability here; the user guide contains an example to the second one.
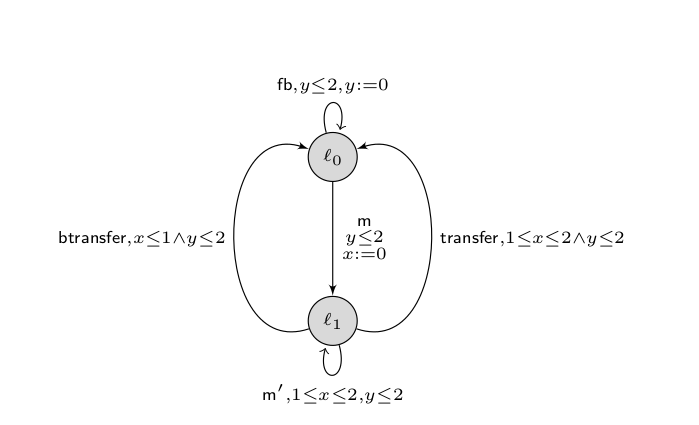
Let us describe a simple system that is not shrinkable. We consider the timed automaton A of the figure below. The system has to give a feedback (fb) at least every 2 time units, through the self-loop on ℓ0. At any time, it can receive a message m, which it can transfer to another system after a delay of at least 1 and at most 2. In fact, let us assume that the target system only listens between this time interval. If the message is sent too early or too late, it will be lost. In addition, while the system is in the state ℓ1 preparing for transferring the message, it can decide to send the message to a buffer by realizing the btransfer action as long as x≤ 1. The sytem may also receive a dupplicate (m′) of the message while 1≤ x≤ 2.
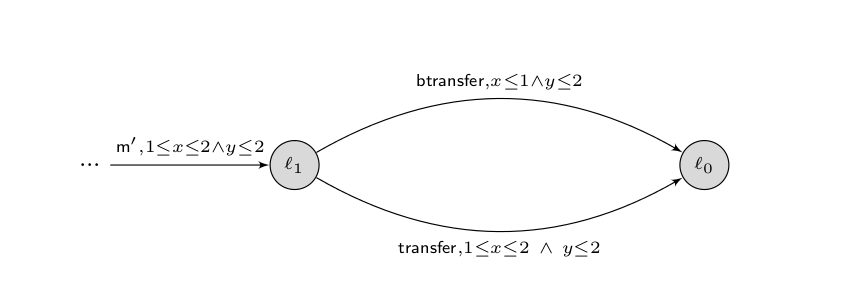
To simplify the discussion, we will only concentrate on a simple behaviour of 2, and summarize it as the timed automaton in the figure below. This timed automaton consists of the unfolding of the above one for two transitions from ℓ1. By investigating the state space of 2, one can see that it contains a branching: at ℓ1, both btransfer and transfer actions are available. The state space is illustrated in the figure below. On the other hand, under any shrinking, the branching btransfer and transfer is disabled (the right of the figure). This means that a controller that waits for the repetition of the message before making the decision between btransfer and transfer is not robust. Therefore, the timed automaton is not shrinkable w.r.t. its own time-abstract behaviour. Note however that the shrunk automaton does contain the behaviours m·m′· transfer and m·m′· btransfer so if the branching is not important, one can eliminate the branching in the time-abstract bisimulation quotient and prove shrinkability w.r.t. this smaller finite automaton.
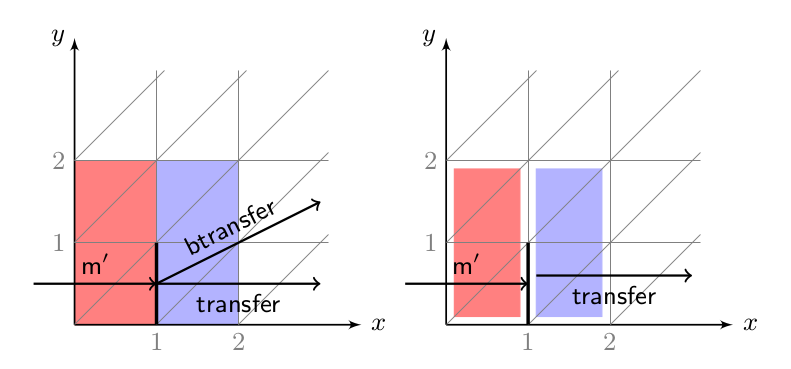
| The figure on left illustrates the behaviour in the original timed automaton, while on the right, the behaviour of the shrunk automaton is given. The red area is the guard of btransfer, while the blue area is the guard of transfer. The thick black segment is a set of states reachable after the action m′. From this set, both actions transfer and btransfer are available in the original timed automaton, while the latter is disabled in the shrunk automaton. Hence, the branching disappears under any shrinking. |