


4 Méthodes de preuve automatique
La question que nous traitons maintenant est : étant donnée une
formule F, F est-elle valide ? (Ou de façon
équivalente, F, ou ¾® F, est-il prouvable ?)
Traditionnellement, ce problème est présenté en niant F, et
en demandant si ¬F est insatisfiable. Nous n'adopterons pas
ce point de vue, que nous trouvons peu naturel. Sa justification est
essentiellement historique.
4.1 Tableaux
La méthode des tableaux est due à Beth, Hintikka et Smullyan dans
les années cinquante et soixante. On peut la comprendre
sémantiquement, comme un moyen systématique de recherche d'une
interprétation qui ne satisfasse pas F par récursion
structurelle sur F (c'est pourquoi cette méthode est parfois
appelée méthode des tableaux sémantiques). En fait,
cette méthode de recherche de ce que nous appellerons des contre-modèles de F suit exactement la preuve du
théorème 24. Autrement dit, les
tableaux sont plus faciles à comprendre syntaxiquement, comme une
recherche systématique d'une preuve sans coupure dans LK0.
| (a-règles) |
(b-règles) |
| |
| a |
a1 |
a2 |
| +(XÙ Y) |
+X |
+Y |
| -(XÚ Y) |
-X |
-Y |
| -(XÞ Y) |
+X |
-Y |
| +(¬ X) |
-X |
|
| -(¬ X) |
+X |
|
|
|
| b |
b1 |
b2 |
| -(XÙ Y) |
-X |
-Y |
| +(XÚ Y) |
+X |
+Y |
| +(XÞ Y) |
-X |
+Y |
|
Figure 4: Règles de tableaux
Si on laisse de côté la coupure et la contraction, la méthode
des tableaux n'est que l'algorithme qui cherche à construire une
preuve dans LK0 en remontant à partir du but à prouver, et
terminant la preuve par des instances de Ax; cette méthode conclut
à l'invalidité lorsqu'elle dérive un séquent ne contenant que
des variables propositionnelles et qui n'est pas une instance de Ax.
Mais la communauté des tableaux utilise souvent un vocabulaire
différent, que nous définissons maintenant.
Les règles de LK0 peuvent être classées en deux
catégories (cf. figure 4). Certaines, comme
ÙR, ont éventuellement plusieurs prémices, mais aucune n'est
plus grosse que la conclusion : on les renomme a-règles, elles correspondent respectivement à ÙR,
ÚL, ÞL, ¬R et ¬L. Toutes les autres ont une
prémice unique qui est plus grosse que leur conclusion : ce sont les
b-règles, elles correspondent respectivement à
ÙL, ÚR, ÞR. Ensuite, les méthodes de tableaux
travaillent sur des ensembles de chemins à travers des formules
signées, c'est-à-dire des couples (+, F) ou (-, F), que
l'on notera respectivement +F et -F :
Définition 27 [Chemins]
L'ensemble des chemins à travers F est le plus petit
ensemble d'ensembles de formules signées tel que :
- {+F} est un chemin;
- si C est un chemin, et a est une formule signée
dans C de type a, alors (C\{a}) È
{a1} et (C\{a}) È {a2}
sont des chemins (où a1 et a2 sont
définies comme dans la figure 4; dans le cas de
la négation, il n'y a que le premier chemin);
- si C est un chemin, et b est une formule signée dans
C de type b, alors (C\{b}) È
{b1,b2} est un chemin (où b1 et
b2 sont définis comme dans la
figure 4.)
Une stratégie d'expansion f est une application envoyant
chaque chemin C possédant au moins une formule signée non
atomique vers une telle formule.
Un chemin C est clos s'il existe une formule +F' dans
C telle que -F' soit aussi dans C. Un tableau est
un ensemble de chemins. Il est clos si et seulement si tous
ses chemins sont clos.
Les chemins sont des séquents, où les formules négatives sont
sur la gauche, et les formules positives sont sur la droite. Les
règles d'expansion (a et b) correspondent aux huit
règles de LK0 sauf Ax et Cut. Et un chemin clos est une
instance de Ax. Remarquer que le choix de la formule à expanser
dans un chemin est arbitraire, autrement dit toute stratégie de
choix d'une telle formule est capable de prouver tous les
théorèmes. (Cf. l'utilisation de la stratégie f dans la
preuve de complétude de LK0.)
La distinction entre les deux catégories de règles est due au fait
que les a-règles sont des règles de ramification,
qui peuvent augmenter le nombre de chemins à clore, mais
n'augmentent jamais le nombre de formules dans un chemin; alors que
les b-règles sont des règles de prolongation, qui
n'augmentent pas le nombre de chemins à clore, mais rallongent le
chemin courant.
Une réalisation classique de la méthode des tableaux est la
suivante. Nous utilisons une liste pour représenter le chemin
courant : une liste est soit la liste vide [] soit un couple x::l
d'un objet x et d'une liste l. Soit [x1,...,xn] la
liste contenant n objets x1, ..., xn, autrement dit
x1 ::... ::xn ::[]. Nous définissons une fonction
prouve prenant en arguments une liste de formules signées
représentant le séquent à prouver (autrement dit, le chemin
courant, et que nous voulons expanser en des chemins clos) :
- si l contient à la fois +F et -F pour un certain
F, retourner ``oui'';
- sinon, si l ne contient que des variables signées, retourner
``non'';
- sinon, appliquer la stratégie d'expansion pour choisir une
formule signée non atomique F dans l, et soit l' la liste
l sans F.
- si F est une formule de type a (avec n
ai-formules F1, ..., Fn, où n=1
ou n=2), alors retourner ``oui'' si
prouve(F1::l'), ...,
prouve(Fn::l') retournent tous ``oui''; sinon
retourner ``non''.
- si F est une formule de type b (se décomposant en
formules F1, F2), alors retourner
prouve(F1::F2::l').
Donc, pour savoir si F est un théorème, nous lançons
prouve([+F]), et lisons la réponse.
La stratégie d'expansion est utilisée pour choisir une formule
signée F non variable dans l au troisième point ci-dessus.
C'est un léger abus, car la stratégie est maintenant une fonction
des listes, non des ensembles de formules signées vers les formules
signées. En pratique, l est typiquement codée par une liste
l de formules en attente de traitement, une liste pos de
formules atomiques positives (+A), et une liste neg de
formules atomiques négatives (-A). En détail et en Caml, sur un
langage de formules simplifié ne comprenant que le Ú et le
¬:
open List;;
type atom = string;;
type form = A of atom
| OU of form * form
| NON of form;;
type sform = POS of form | NEG of form;;
let rec prouve1 l pos neg =
match l with
[] -> false
| POS (A x)::l' -> mem x neg || prouve1 l' (x::pos) neg
| NEG (A x)::l' -> mem x pos || prouve1 l' pos (x::neg)
| POS (OU (f, g))::l' -> prouve1 (POS f::POS g::l') pos neg
| NEG (OU (f, g))::l' -> prouve1 (NEG f::l') pos neg &&
prouve1 (NEG g::l') pos neg
| POS (NON f)::l' -> prouve1 (NEG f::l') pos neg
| NEG (NON f)::l' -> prouve1 (POS f::l') pos neg
;;
let prouve f = prouve1 [POS f] [] [];;
La méthode des tableaux a la propriété importante suivante :
Théorème 28 [Correction, complétude] Les tableaux sont corrects et complets pour toute stratégie :
l'expansion du tableau +F termine sur un tableau clos si et
seulement si F est valide.
Preuve : Conséquence du théorème 23 et des
arguments du théorème 24, portant sur
des listes plutôt que des ensembles pour ce qui est de la
complétude.
¤
On notera bien que les termes ``correct'' et ``complet'' portent ici
sur les procédures de recherche de preuve, pas sur les systèmes de
preuve. Une méthode de recherche de preuve est correcte si elle ne
retourne ``oui'' que lorsque son entrée est une tautologie. Elle
est complète si elle retourne ``oui'' dès que son entrée est une
tautologie. La distinction est subtile : une méthode de recherche
de preuve est une procédure, alors qu'un système de preuve
n'est qu'une collection de règles, sans interprétation
calculatoire a priori. Plus concrètement, dire que LK0 sans
Cut est complet dit que toute tautologie a une preuve, mais nous ne
savons pas dans quel ordre appliquer les règles, c'est-à-dire
quelle stratégie utiliser. Dire que prouve est complet nous
en dit plus, à savoir que l'ordre particulier dans lequel
prouve déplie une dérivation finira par produire une preuve
si le but est une tautologie; ici, ceci est une conséquence du fait
que n'importe quel ordre d'application des règles de preuve
(n'importe quelle stratégie) finit par aboutir à une preuve.
Théorème 29 [Terminaison] Soit F une formule propositionnelle. L'expansion du tableau
+F termine, quelle que soit la stratégie utilisée.
Preuve : L'expansion d'un tableau construit un nouveau noeud dans l'arbre
défini au théorème 24 à chaque
étape. Comme cet arbre est fini, la procédure termine.
¤
L'intérêt des tableaux est qu'ils sont très simples à
réaliser, et que les étapes fondamentales de calcul peuvent être
effectuées très rapidement. De plus, ses besoins en espace sont
modestes : nous n'avons besoin que d'une pile pour gérer la
récursion dans prouve, et sa profondeur est au plus la taille
de la formule à prouver. Cependant, comme la taille d'un tableau
totalement expansé est en général une exponentielle de la taille
de la formule à prouver, prouver un théorème par une méthode
de tableaux peut prendre quelque temps. (Ce problème est en fait
général à toutes les méthodes de preuve.)
Plus spécifiquement, le principal point faible des tableaux est
qu'il développe chaque chemin du tableau complètement
indépendamment des autres. En particulier, si nous choisissons
d'expanser la même formule dans deux chemins différents, nous
faisons le même travail deux fois, et gâchons du temps.
4.2 Résolution propositionnelle
La méthode de résolution, inventée en 1965 par J. Alan Robinson
dans le cadre plus général de la recherche de preuve au premier
ordre, et la méthode de Davis-Putnam-Logemann-Loveland, inventée
en 1960 par Martin Davis et Hillary Putnam et améliorée en 1963
par Martin Davis, George Logemann et Donald Loveland, aussi dans le
cadre du premier ordre, nécessitent toutes les deux une étape
préliminaire. Pour prouver F (ou pour réfuter ¬F),
nous mettons d'abord ¬F en forme normale conjonctive (voir
plus bas). Une façon d'expliquer la résolution propositionnelle
est alors d'interpréter la forme normale conjonctive de ¬F
comme un ensemble de séquents, à partir duquel nous essayons de
dériver le séquent absurde (vide) ¾® en utilisant les
règles de LK0.
Définition 30 Une formule F est en forme négation-normale (nnf) si
et seulement si elle est construire avec les connecteurs Ù,
Ú, ¬ uniquement, et si toute sous-formule niée
¬F' est telle que F' est une variable propositionnelle.
(Les négations ne gouvernent pas les formules composites.)
Un atome est un autre nom pour une variable
propositionnelle. Un littéral est une formule de la forme
A ou ¬ A, où A est un atome.
Une formule F est en forme normale disjonctive (dnf) si
et seulement si elle est en nnf et aucune disjonction
n'apparaît comme argument d'une conjonction. (C'est-à-dire
que F est une disjonction n-aire de clauses
conjonctives, qui sont des conjonctions m-aires de
littéraux.)
De façon symétrique, une formule F est en forme
normal conjonctive (cnf) si et seulement si elle est en nnf et
aucune conjonction n'apparaît comme argument d'une disjonction.
(C'est-à-dire que F est une conjonction n-aire de clauses disjonctives, qui sont des disjonctions m-aires de
littéraux.)
La clause disjonctive vide est notée  .
.
Pour abréger, nous dirons clause au lieu de clause
disjonctive. Une clause est donc une disjonction de littéraux.
Nous pouvons interpréter les clauses comme des séquents en mettant
à droite tous les littéraux positifs A, et à gauche tous les
atomes A venant de littéraux négatifs ¬ A, et en
éliminant les doublons. Ceci établit une correspondance entre
clauses et séquents atomiques, c'est-à-dire séquents ne
contenant que des atomes. ( correspond alors à ¾® .)
À partir de maintenant, clause voudra dire séquent,
écrit avec Ú et ¬ au lieu de la notation à flèche
précédente. C'est à strictement parler un abus de langage,
d'autant plus que les contractions (remplacer FÚF par
F) sont sous-entendues dans les clauses. Nous utilisons cette
notation parce qu'elle est traditionnelle, et parce qu'elle apporte
des intuitions sémantiques utiles.
correspond alors à ¾® .)
À partir de maintenant, clause voudra dire séquent,
écrit avec Ú et ¬ au lieu de la notation à flèche
précédente. C'est à strictement parler un abus de langage,
d'autant plus que les contractions (remplacer FÚF par
F) sont sous-entendues dans les clauses. Nous utilisons cette
notation parce qu'elle est traditionnelle, et parce qu'elle apporte
des intuitions sémantiques utiles.
Voici un algorithme pour mettre une formule F en nnf : d'abord,
réécrire toutes les sous-formules F'ÞF'' sous la forme
¬F'ÚF'', de sorte à obtenir une formule équivalente
n'utilisant que Ù, Ú et ¬. Ensuite utiliser les
identités de de Morgan :
| ¬ (F' Ù F'') est logiquement équivalent à (¬ F') Ú (¬ F'') |
| ¬ (F' Ú F'') est logiquement équivalent à (¬ F') Ù (¬ F'') |
pour pousser les négations vers l'intérieur de la formule.
Maintenant, si F est en nnf, nous la transformons en cnf en
réécrivant toutes les sous-formules F'Ú (F1Ù
F2) en (F'Ú F1)Ù (F'Ú F2) et
(F1Ù F2)Ú F' en (F1Ú F')Ù
(F2Ú F'). Le processus termine, mais nous ne le
prouverons pas (exercice).
Mettant à profit notre compréhension des clauses comme des
séquents, observons que si l'on cherche une preuve sans coupure ni
contraction de ¾® F en appliquant les règles de LK0
au maximum, on aboutit à un ensemble de séquents atomiques dont la
conjonction est équivalente à F. Dans le langage des
tableaux, développer un tableau pour +F jusqu'à ce que tous
les chemins non clos restant soient atomiques : la conjonction de tous
ces chemins, où chaque chemin est vu comme une disjonction de
littéraux (+A pour A et -A pour ¬ A), est équivalent
à F, et est donc une cnf pour F.
Nous avons ensuite :
Théorème 31 [Résolution]
Soit F une formule en cnf, et considérons F comme un
ensemble S de séquents atomiques. Alors F est
insatisfiable si et seulement si le séquent vide ¾® est
déductible de S et de la règle Cut seulement.
Preuve : La correction (si ¾® est déductible par Cut de S, alors
F est insatisfiable) est due à l'observation suivante : si
G ¾® F',D et G',F' ¾® D'
sont coupés sur F' pour donner G,G' ¾®
D,D', alors toute interprétation r qui satisfait
les deux premiers doit aussi satisfaire la dernière. Donc si
F était satisfiable, par récurrence sur la longueur de la
dérivation de ¾® à partir de S, nous montrerions que
¾® est satisfiable, ce qui est absurde.
Montrons maintenant la complétude, c'est-à-dire la réciproque.
Figure 5: Un arbre de décision
Nous construisons un arbre de décision (figure 5).
Soient A1, ..., An les variables libres de F.
Nous définissons les noeuds de l'arbre à profondeur i (à
partir de la racine), 0£ i£ n, comme toutes les suites
A1r, ..., Air, où r est une affectation
quelconque, et Ar dénote A si r(A) = T et ¬
A sinon. Si A1r, ..., Air est un noeud,
soit i=n et il s'agit d'une feuille, soit i<n, et il a
deux fils A1r, ..., Air, ¬ Ai+1
et A1r, ..., Air, Ai+1. Appelons une
telle suite A1r, ..., Air une interprétation partielle. Si i=n, il s'agit d'une interprétation totale. (Ces dernières sont les
interprétations au sens intuitif, envoyant Ai vers T
si Air=Ai, vers F si Air=¬
Ai.)
Supposons que S, en tant que conjonction des séquents qui lui
appartiennent, est insatisfiable, c'est-à-dire que pour toute
interprétation r, il existe un CÎ S tel que non
r|= C. Pour toute interprétation totale, il y a au
moins un séquent dans S qui n'est pas satisfait par
l'interprétation correspondante r. Nous appelons noeud d'échec pour un séquent C dans S tout noeud
le plus haut possible dans l'arbre tel qu'aucune interprétation
totale passant par ce noeud ne satisfasse C. Nous
définissons ensuite l'arbre de décision clos de S
comme étant l'arbre de décision de départ, coupé à chaque
noeud d'échec (autrement dit, les noeuds d'échec
deviennent des feuilles). Remarquons que toute interprétation
totale doit traverser au moins un noeud d'échec, et donc les
feuilles de l'arbre clos sont exactement les noeuds d'échec de
l'arbre de départ.
Ensemble de clauses:
B,
AÚ¬
B, ¬
AÚ C, ¬
C.
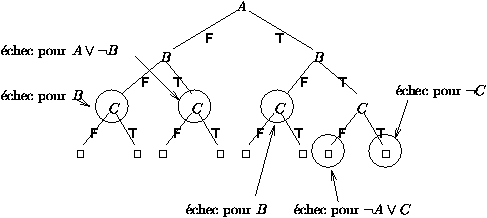
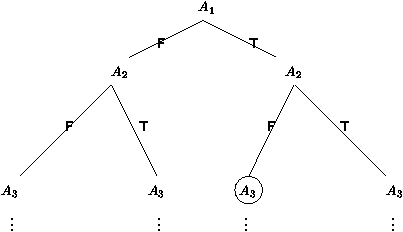
Figure 6: Un arbre de décision, avec noeuds d'échec
Par exemple, considérons la figure 6, où S
consiste en ¾® B, B ¾® A, A ¾® C, C
¾® (en tant que clauses, B, AÚ¬ B, ¬ AÚ C,
¬ C). Notre énumération des atomes est A1 = A, A2 =
B, A3 = C. Le noeud dans un rond le plus à gauche
(l'interprétation partielle ¬ A,¬ B) est un noeud
d'échec pour le séquent ¾® B (la clause B) parce que
B est rendue fausse à ce noeud, mais à aucun noeud plus
haut. Les noeuds d'échec sur cet exemple sont précisément
ceux entourés d'un rond dans la figure 6, et
l'arbre clos est le sous-arbre situé au-dessus de ces noeuds
d'échec.
Nous définissons maintenant les noeuds d'inférence
comme étant les noeuds de l'arbre clos qui ont deux noeuds
d'échec comme fils. Nous affirmons que si l'arbre clos a plus
d'un noeud (si la racine n'est pas un noeud d'échec), alors
il y a au moins un noeud d'inférence.
En effet, soit n le nombre de noeuds dans l'arbre clos (en
incluant les feuilles), et prouvons l'affirmation par récurrence
sur n. Comme la racine n'est pas un noeud d'échec, n³
3. Si n=3, alors la racine est un noeud d'inférence.
Sinon, n>3 et supposons l'affirmation prouvée pour tous les
arbres clos avec au moins 3 noeuds, et au plus n-1 noeuds.
Notre arbre clos a n noeuds, n>3 : la racine n'est pas un
noeud d'échec, et un de ses fils n'est pas non plus un noeud
d'échec; le sous-arbre dont la racine est ce fils a donc au moins
3 noeuds, et strictement moins de n noeuds, donc par
hypothèse de récurrence il contient un noeud d'inférence.
Donc l'arbre clos total contient un noeud d'inférence.
Par définition, si un noeud d'inférence N est étiqueté
par une variable propositionnelle A (c'est-à-dire A égale
Ai et N est une interprétation partielle A1r,
..., Ai-1r), alors il existe un séquent dans S pour
lequel le fils de gauche du noeud est un noeud d'échec (et
ce séquent doit être de la forme G ¾® A,D), et
de même il existe un séquent dans S pour lequel le fils de
droit du noeud est un noeud d'échec (et il doit être de la
forme G',A ¾® D').
Par exemple, sur la figure 6, les noeuds
d'inférence sont le noeud B le plus à gauche (clause de
gauche B, clause de droite AÚ¬ B), et le noeud C le
plus à droite (clause de gauche ¬ AÚ C, clause de droite
¬ C).
Produisons alors la clause G,G' ¾® D,D',
qui est le résultat de l'application de Cut sur ces séquents, et
ajoutons le à S. Ce faisant, nous obtenons un nouvel ensemble
S' de séquents, qui est insatisfiable. Remarquons que tout
noeud d'échec pour S est un noeud d'échec ou est
en-dessous d'un noeud d'échec de S'. Remarquons aussi que le
noeud d'inférence N choisi dans S est maintenant noeud
d'échec pour S' (prouvez-le en exercice), de sorte que l'arbre
clos pour S' est strictement plus petit que celui pour S. (Dans
l'exemple, si l'on coupe entre B et AÚ¬ B sur le noeud
d'inférence de gauche, ceci produit A comme nouvelle clause, et
produit l'arbre de décision de la figure 7.)
Figure 7: L'arbre de décision, après application de Cut
En somme, si nous prenons comme valeur initiale de S l'ensemble
des clauses représentant F, nous fabriquons, par
l'application de Cut entre des clauses aux noeuds d'inférence,
des ensembles insatisfiables de clauses de plus en plus gros et
ayant des arbres clos de plus en plus petits. Après un nombre
fini de telles opérations, l'arbre clos sera donc réduit à sa
racine. Mais si la racine est un noeud d'échec, c'est qu'une
clause doit être rendue fausse par l'interprétation partielle
vide. Comme toutes les clauses que nous produisons sont atomiques,
une telle clause ne peut être que la clause vide. Ainsi, la
clause vide a dû être engendrée en un nombre fini
d'application de Cut à partir de S.
¤
Ce théorème est surprenant : si une formule F est prouvable,
alors soit S l'ensemble des séquents atomiques correspondant à
une cnf pour ¬F. En utilisant la règle Cut, nous pouvons
montrer que F est prouvable à partir de LK0 si et
seulement si ¾® est dérivable à partir de LK0+S
(le système de preuve contenant les règles de LK0plus tous
les séquents de S vus comme de nouveaux axiomes). Le
théorème 31 est ainsi en quelque sort le
contraire du théorème 26 : au lieu d'éliminer
les coupures, nous éliminons toutes les règles de LK0 sauf
Cut. Nous expliquerons cette énigme lorsque nous examinerons le processus
d'élimination des coupures.
Pour appliquer le théorème 31, Robinson
avait proposé une variante de l'algorithme suivant. Étant donné
un ensemble S de clauses pour ¬F, où F est la formule
à prouver :
- Soit S0 = S, et n = 0 (n sera appelé le niveau,
et Sn l'ensemble des clauses au niveau n).
- Si Sn contient la clause vide, retourner ``oui''.
- Sinon, calculer l'ensemble des resolvants de clauses de
Sn (un résolvant est le résultat d'une coupure sur deux
clauses), telles que les clauses coupées (les prémices) ne sont
pas toutes deux dans Sn-1 si n³ 1; (sinon, on
refabriquerait les clauses qui sont déjà dans Sn;) les
ajouter à Sn pour obtenir un nouvel ensemble Sn+1.
- Si Sn+1=Sn, alors retourner ``non''.
- Sinon, poser n égale n+1, et retourner à l'étape 2.
Cet algorithme est appelé résolution par saturation de
niveaux, parce que Sn est l'ensemble de toutes les
conséquences de S déductibles en appliquant Cut au plus n
fois.
Cet algorithme est très inefficace. Le problème ne tient pas tant
à la comparaison entre les ensembles Sn et Sn+1, mais
dans le fait que les résolvants qui sont calculés à l'étape 3
peuvent contenir énormément de redondance : de nombreuses
tautologies (séquents Ax) et des clauses qui avaient déjà
été fabriquées sont refabriquées constamment. En fait, la
résolution est une très mauvaise méthode de recherche de preuve
propositionnelle, mais elle est plus intéressante au premier ordre.
4.3 La méthode de Davis-Putnam-Logemann-Loveland
Nous arrivons aux méthodes sémantiques. Ces méthodes sont, en
pratique, parmi les procédures correctes, complètes et terminantes
les plus rapides que l'on connaît aujourd'hui.
L'idée de la méthode de Davis-Putnam-Logemann-Loveland est la
suivante. Elle prend encore en entrée un ensemble S de clauses
représentant ¬F, où F est la formule à prouver.
F est valide si et seulement si S est insatisfiable. Si S
est vide, alors S est satisfiable, donc F est invalide. Si S
contient la clause vide, il est insatisfiable, donc F est valide.
Sinon, nous choisissons une variable propositionnelle libre A dans
S, et essentiellement nous remplaçons A par vrai (resp. faux)
dans S, et simplifions le tout, ce qui donne un ensemble S1
(resp. S2) de clauses : S est alors satisfiable si et
seulement si S1 ou S2 est satisfiable.
Ce qui fait que la méthode de Davis-Putnam-Logemann-Loveland est
efficace est qu'elle identifie un certain nombre de cas particuliers
où nous n'avons pas à séparer S en S1 et S2 selon la
valeur de la variable A. En effet, cette séparation multiplie le
nombre de sous-problèmes à résoudre par 2 pour chaque variable
propositionnelle, et c'est la cause de l'explosion exponentielle du
nombre de sous-problèmes à résoudre.
Les règles sont les suivantes :
Définition 32 [Tautologies]
Une clause est appelée une tautologie si et seulement si
elle contient A et ¬ A, où A est une variable.
Remarquer en effet qu'une clause est valide si et seulement si elle
contient à la fois A et ¬ A, pour une certaine variable A.
Définition 33 [Séparation (splitting)] Soit S un ensemble de clauses non tautologiques, et A une
variable propositionnelle.
Définissons S[T/A] comme l'ensemble S d'où toutes les
clauses de la forme CÚ A (contenant A comme littéral
positif) ont été supprimées, et où toutes les clauses
CÚ¬ A ont été remplacées par C.
Définissons S[F/A] comme l'ensemble S où toutes les clauses
de la forme CÚ A ont été remplacées par C, et d'où
toutes les clauses CÚ¬ A ont été supprimées.
Remarquer qu'une affectation r telle que r(A)=T (resp.
F) satisfait S si et seulement si elle satisfait S[T/A]
(resp. S[F/A]), et que ces derniers n'ont plus A comme variable
libre.
Définition 34 [Clause unitaire] Une clause C est dite unitaire si elle contient exactement
un littéral.
Les clauses unitaires sont intéressantes parce que si S contient
une clause unitaire, disons A, alors S est satisfiable si et
seulement si A est satisfiable. Toute affectation satisfaisant S
doit attribuer vrai à A, donc S est satisfiable si et seulement
si S[T/A] l'est. (Si la clause unitaire est de la forme ¬ A,
S est satisfiable si et seulement si S[F/A] l'est.) En
particulier, si S contient une clause unitaire, nous n'avons pas
besoin d'effectuer une séparation sur A, car il n'y a qu'un choix
possible.
Définition 35 [Littéraux purs] Un littéral A (resp. ¬ A) est dit pur dans un
ensemble de clauses S si et seulement si ¬ A (resp. A)
n'apparaît dans aucune clause de S.
Une clause est pure dans S si elle contient un littéral
pur dans S.
Supposons que A (resp. ¬ A) est pur dans S. S[T/A]
(resp. S[F/A]) est alors un sous-ensemble de S, donc si S est
satisfiable, alors S[T/A] (resp. S[F/A]) l'est aussi.
Réciproquement, si S[T/A] (resp. S[F/A]) est satisfiable,
soit r une affectation satisfaisant toutes ses clauses, et
r' l'affectation envoyant A vers T (resp. F) et
toutes les autres variables B vers r(B). Alors r'
satisfait toutes les clauses de S; en effet, pour chaque clause dans
C, soit A n'apparaît pas dans C et C est dans S[T/A]
(resp. S[F/A]), donc r' satisfait C, ou C est de la forme
C'Ú A (resp. C'Ú¬ A), et par déefinition de r' en
A, r' satisfait C de nouveau.
Une autre façon de le dire est que si S contient une clause
pure, alors S sans cette clause pure est satisfiable si et seulement
si S est satisfiable. Nous pouvons donc éliminer les clauses
pures de S sans changer sa satisfiabilité. On notera de plus
qu'éliminer des clauses pures peut rendre d'autres clauses pures:
par exemple, parmi les trois clauses A Ú ¬ B, ¬ A Ú
¬ B, B Ú C, la troisième est pure car ¬ C
n'apparaît pas dans l'ensemble de clauses: on peut donc
l'éliminer; mais alors les deux premières clauses deviennent pures
elles-mêmes, car B n'apparaî plus nulle part; on conclut donc
immédiatement que ces trois clauses forment un ensemble satisfiable.
(Exercice: reconstruire une affectation satisfaisant ces trois
clauses.)
La procédure de Davis-Putnam-Logemann-Loveland fonctionne comme suit.
Au départ, S est un ensemble fini de clauses :
- si S est vide, retourner ``satisfiable''.
- si S contient la clause vide, retourner ``insatisfiable''.
- si S contient une tautologie (definition 32)
ou une clause pure, l'éliminer de S et aller en étape 1.
- si S contient une clause unitaire A (resp. ¬ A),
remplacer S par S[T/A] (resp. S[F/A]), et aller en étape
1.
- sinon, choisir une variable libre A dans S. Appliquer la
procédure de Davis-Putnam-Logemann-Loveland récursivement sur
S[T/A] et S[F/A]. Retourner ``satisfiable'' si l'un des
résultats était ``satisfiable'', et retourner ``insatisfiable''
sinon.
On peut beaucoup améliorer la dernière étape. Tout d'abord,
nous pouvons déjà appliquer la procédure de
Davis-Putnam-Logemann-Loveland sur S[T/A], et retourner
``satisfiable'' immédiatement si le résultat est ``satisfiable'',
sinon nous appliquons la procédure de Davis-Putnam-Logemann-Loveland
sur S[F/A]. Nous pouvons aussi décider d'appliquer
Davis-Putnam-Logemann-Loveland sur S[F/A] en premier, et ensuite
éventuellement sur S[T/A], ou lancer les deux en
parallèle...
Sur un ordinateur séquentiel, nous avons besoin d'une stratégie
pour savoir lequel des deux tester en premier. Nous avons aussi
besoin d'une stratégie pour choisir la variable A dans la
dernière étape. Les choix de stratégie peuvent avoir beaucoup
d'influence sur la rapidité de l'algorithme à conclure. Les
bonnes heuristiques sont typiquement de choisir A de sorte que le
nombre de clauses dans lesquelles A apparaît multiplié par le
nombre de clauses dans lesquelles ¬ A apparaît est maximal
(si nous devons effectuer une séparation, séparons au moins sur
une variable qui a le plus d'influence sur l'ensemble de clauses), et
de tester S[T/A] d'abord s'il y a plus de clauses contenant A que
de clauses contenant ¬ A, et S[F/A] sinon. (Si nous devons
effectuer une séparation, testons d'abord l'ensemble qui a le moins
de clauses.) Une stratégie plus évoluée est la règle de
Jeroslow-Wang, qui consiste à choisir un littéral L qui maximise
Si 2-ni, où i parcourt les clauses contenant L et
ni est la longueur de la clause i. Consulter
[HV95] pour une discussion.
Un autre point important est comment coder la méthode de
Davis-Putnam-Logemann-Loveland efficacement. La réalisation
traditionnelle n'efface ni ne modifie aucun clause, mais cherche une
affectation qui satisfasse l'ensemble des clauses. Soit r une
affectation partielle, à savoir un ensemble de littéraux
tels que A et ¬ A ne sont jamais simultanément dans r.
(On retrouve la notion habituelle d'affectation quand, pour chaque
A, soit A soit ¬ A est dans r.) Un littéral L est
satisfait par une affectation partielle r si L Î r; une
clause C est satisfaite par r si C Ç r ¹ Ø;
et un ensemble de clauses S est satisfait par r si toutes ses
clauses sont satisfaites par r. L'algorithme tente ensuite de
trouver une affectation (partielle) r satisfaisant S.
Il organise les clauses sous forme d'une matrice creuse, où les
lignes sont des clauses et les colonnes sont repérées par les
variables propositionnelles : si A est une variable
propositionnelle, la colonne A est la liste de toutes les clauses
où A ou ¬ A apparaît. En plus, chaque clause est munie
d'attributs entiers comptant le nombre de littéraux qui sont vrais
(satisfaits), resp. faux (dont la négation est satisfaite), resp.
non affectées par l'affectation partielle courante r. Pour
ajouter un littéral L (A or ¬ A) à r, comme lors des
étapes de séparation, de propagation des littéraux unitaires ou
d'élimination de clauses pures, on parcourt la colonne A, et on
met à jour les compteurs. Si le compteur de littéraux vrais et le
compteur de littéraux non affectés sont tous les deux nuls dans
une clause, alors échouer, et revenir (backtracker) au
dernier point où une séparation a été effectuée. Pour
gérer les clauses unitaires, on maintient une pile de littéraux
unitaires : chaque fois que le nombre de littéraux non affectés
dans une clause devient un et que le nombre de littéraux vrais est
toujours nul, on empile le seul littéral restant sur la pile, à
moins que sa négation ne soit déjà sur la pile. (On backtracke
dans ce dernier cas.) On peut aussi gérer les clauses pures en
conservant dans chaque colonne le nombre d'occurrences positives,
resp. négatives de variables dans chaque clause.
4.4 Diagrammes de décision binaire
Une autre idée qui fonctionne pour prouver des formules
propositionnelles et qui vient d'idées sémantiques est celle des
diagrammes de décision binaire, ou BDD. Le créateur
des BDD tels que nous les connaissons aujourd'hui est Randall E.
Bryant en 1986. Cependant, les BDD sont juste des arbres de
décision avec quelques astuces bien connues en plus, et les arbres
de décision remontent à George Boole (1854), si pas plus tôt.
Les idées sont très simples, mais les réalisations informatiques
sont usuellement plus complexes qu'avec les méthodes
précédentes.
En gros, les astuces qui font que les BDD fonctionnent sont : d'abord,
au lieu de représenter les arbres de décision comme des arbres en
mémoire (où il y a un unique chemin de la racine à n'importe
quel noeud), nous les représentons comme des graphes
orientés acycliques ou DAG, autrement dit nous
partageons tous les sous-arbres identiques. Ensuite, nous utilisons
la règle de simplification suivante : si un sous-arbre a deux fils
identiques, alors remplacer le sous-arbre par ce fils;
essentiellement, ce sous-arbre signifie ``si A est vrai, alors
utilise le fils de droite; si A est faux, utilise le fils de
gauche'': comme les fils de gauche et de droite coincident, il n'y a
pas lieu d'effectuer une sélection fondée sur la valeur de A.
Enfin, nous ordonnons les variables dans un ordre total donné <,
et exigeons que, si nous descendons dans le BDD sur n'importe quel
chemin, nous rencontrons les variables en ordre croissant. Cette
dernière propriété assurera que les BDD sont des représentants canoniques de formules à équivalence logique
près, c'est-à-dire que si F et F' sont deux formules
équivalentes, alors leurs BDD construits sur le même ordre sont
identiques.
À la base, les BDD sont soit T (vrai), F (faux) ou ``si A
alors F+ sinon F-'', où F+ et F- sont des
BDD distincts. Nous notons cette dernière forme A¾®
F+; F-, ou sous forme d'arbre :
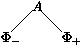
Cette représentation simple nous permet de construire des BDD
morceau par morceau. Par exemple, pour construire le BDD de F
Ù F', il suffit de combiner les BDD de F et de F'.
Si le BDD de F est ``si A alors F+ sinon F-'', et
celui de F' est ``si A alors F'+ sinon F'-''; alors
le BDD de FÙ F' est simplement ``si A alors F+Ù
F'+ sinon F-Ù F'-'', où les deux conjonctions
F+Ù F'+ et F-Ù F'- sont calculées
récursivement. Le même principe s'applique aux disjonctions,
implications, négations, et ainsi de suite, et est appelé le
principe de décomposition de Shannon (cf. plus bas).
On peut donc calculer les BDD de formules de bas en haut : par
exemple, pour calculer le BDD de (AÙ B) Ú C, nous calculons
celui de A, à savoir A¾® T; F, celui de B, à
savoir B¾® T; F, puis nous calculons leur
conjonction, puis la disjonction de ce dernier avec le BDD de C. Le
fait que les BDD sont des formes canoniques nous assure que la formule
de départ est valide si et seulement si son BDD est exactement T.
Définissons maintenant les BDD plus formellement. Soit T (vrai)
et F (faux) deux nouveaux symboles (à ne pas confondre avec les
valeurs de vérité T et F, bien que ce soit ce
qu'elles représentent.)
Lemme 36 [Shannon] La sémantique de T est [T]=T, celle de F est
[F]=F.
Pour toute formule F, et toute variable propositionnelle A,
F est équivalente à (AÞF[T/A])Ù(¬
AÞF[F/A]), où A n'apparaît libre ni dans
F[T/A] ni dans F[F/A]. Ceci est appelé le
principe de décomposition de Shannon.
Preuve : exercice.
¤
Définition 37 [Graphes de Shannon] Un graphe de Shannon est une formule construite sur les deux
constantes T, F au moyen du seul connecteur ternaire
_¾®_;_. Plus précisément, l'ensemble des
graphes de Shannon est le plus petit ensemble tel que T et F
sont des graphes de Shannon, et tel que, si A est une variable, et
F+, F- sont deux graphes de Shannon, alors
A¾®F+;F- (``si A alors
F+, sinon F-'') est un graphe de Shannon.
A¾®F+;F- sera aussi représenté graphiquement par
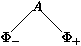 (Remarquer que la branche ``A vrai'' est à droite, alors que la
branche ``A faux'' est à gauche, ce qui est l'ordre inverse de
F+ et F-.)
(Remarquer que la branche ``A vrai'' est à droite, alors que la
branche ``A faux'' est à gauche, ce qui est l'ordre inverse de
F+ et F-.)
Nous devons définir la sémantique. Nous avons déjà défini
[T]r comme T, [F]r comme F. La
formule A¾®F+;F- est censée
représenter la formula (AÞF+) Ù (¬
AÞF-) du principe de décomposition de Shannon, donc
nous posons [A ¾® F+;F-]r =
[F+]r si r(A)=T, et =
[F-]r si r(A)=F.
Nous représentons alors les formules construites avec Ù,
Ú, ¬, Þ, etc. par des graphes de Shannon logiquement
équivalents. Par exemple, la formule (((AÞ B)Ù C)Þ
A)Ú¬ C peut être représentée par le graphe de Shannon
suivant :
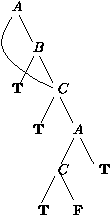
où nous avons dessiné plusieurs noeuds T au lieu d'un dans
l'intérêt de la lisibilité. (Vérifier que ceci est
effectivement équivalent à la formule de départ, en
énumérant toutes les affectations possibles sur A, B, C.)
Ce n'est pas la seule représentation de la formule sous forme de
graphe de Shannon, cependant.
Les graphes (ou arbres) de Shannon ont la propriété suivante, qui
rend le calcul des opérations logiques aisé :
Théorème 38 [Orthogonalité]
Soit F = A¾®F+;F-, F' =
A¾®F'+;F'-.
La négation de F, que nous notons ¬F, est
A¾®¬F+;¬F-. Plus formellement,
ce dernier graphe est satisfait exactement par les affectations qui
ne satisfont pas F.
Pour tout connecteur binaire ° (Ù, Ú, Þ,
Û, respectivement), F ° F'= A ¾®
(F+ ° F'+) ;(F- ° F'-);
plus formellement, ce dernier est satisfait exactement par les
affectations qui satisfont à la fois F et F', resp.
F ou F', resp. F' ou ¬F, resp. à la fois
F et F' ou ni F ni F'.
Preuve : Immédiat.
¤
Nous pouvons faire mieux que les graphes de Shannon, et définir les
BDD :
Définition 39 [BDD] Soit F un graphe de Shannon, et < un ordre strict total des
variables de fv(F).
Nous disons que F est un diagramme de décision
binaire, ou BDD, ordonné par < si et seulement si:
- (Réduit) F ne contient aucun sous-graphe de la forme
A¾®F';F' (avec deux fils identiques);
- (Ordonné) tous les sous-graphes de F de la forme
A¾®F+;F- sont tels que A est
strictement inférieur (pour <) à toutes les variables dans
fv(F+) È fv(F-).
Le BDD de (((AÞ B)Ù C)Þ A)Ú¬ C, avec A<B<C, est
par exemple :
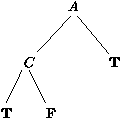
On peut voir un BDD F comme un automate qui décide si une
affectation r donnée satisfait F. En effet, partons de la
racine du BDD et descendons comme suit : lorsque nous sommes à un
noeud étiqueté A (nous considérons un sous-graphe A
¾® F+ ;F-), prenons la branche de droite
(F+ dans l'exemple) si r(A)=T, et la branche de
gauche (F-) si r(A)=F. Ce processus termine
lorsque nous arrivons à une feuille : si cette feuille est T,
alors r satisfait F, alors que si elle est F, r ne
satisfait pas F. Tout ceci est vrai parce qu'essentiellement,
les BDD sont des représentations compactes d'arbres de décision.
Les BDD sont des formes canoniques des formules modulo équivalence logique
(ce que les graphes de Shannon n'étaient pas) :
Théorème 40 [Canonicité] Soient F et F' deux BDD construits sur le même ordre
<. Alors F et F' sont logiquement équivalents si et
seulement s'ils sont égaux.
Preuve : S'ils sont égaux, leur équivalence logique est claire.
Réciproquement, supposons F et F' logiquement
équivalents. Nous montrons qu'ils sont égaux par récurrence
sur le cardinal de fv(F) È fv(F').
Si n=0, alors F et F' sont dans {T, F}; comme
F et F' sont logiquement équivalents, ils sont soit tous
les deux T soit tous les deux F.
Si n³ 1, soit A la plus petite variable de fv(F) È
fv(F') pour l'ordre < (autrement dit, la variable la plus
haute). Sans perte de généralité, supposons que A est libre
dans F. Comme A est la plus petite variable dans
fv(F), nécessairement F = A ¾® F+ ;
F- pour deux BDD F+ et F-.
Si A n'est pas libre dans F', alors F' est logiquement
équivalent à F+ et F-. En effet, si r |=
F', alors r' |= F', où r' envoie A vers
T et toutes les autres variables B vers r(B); comme
F' est logiquement équivalent à F, r' |=
F; comme r'(A) = T, r' |= F+.
Réciproquement, si r |= F+, alors r' |=
F+ où r' est comme ci-dessus, donc r' |=
F, et par équivalence logique r' |= F'; comme A
n'est pas libre dans F', r |= F'. Donc F'
est logiquement équivalent à F+; et de même, F' est
logiquement équivalent à F-. Par hypothèse de
récurrence (les cardinaux de fv(F+) È fv(F') et de
fv(F-) È fv(F') sont en effet strictement inférieurs
à n), F' égale à la fois F+ et F-. Mais
c'est impossible, parce que F est réduit (F+ ¹
F-).
Donc A est libre aussi dans F', et en fait F' = A
¾® F'+ ; F'- pour deux BDD F'+ et
F'-. Par des arguments similaires à ceux ci-dessus,
F+ est logiquement équivalent à F'+ et F- à
F'-, donc par hypothèse de récurrence F+ = F'+
et F- = F'-. Donc F = F'.
¤
En plus, les BDD de formules sont usuellement compacts. Si une
formule est valide ou insatisfiable, son BDD est T ou F, qui est
évidemment très compact. (Mais les BDD de ses sous-formules, que
nous devons construire pour calculer le BDD de la formule toute
entière, peuvent être bien plus gros.) Mais même lorsqu'ils
sont invalides et satisfiables, les BDD restent généralement
petits. Il y a des exceptions, et dans le pire des cas les BDD
peuvent avoir une taille exponentielle en le nombre de variables
libres dans la formule de départ. (Pour être précis, si n est
ce nombre, le nombre de noeuds dans un BDD ne dépasse pas
2n/n.)
La méthode usuelle (et la mieux connue) pour construire un BDD pour
une formule donnée F est d'utiliser le
théorème 38 pour le construire récursivement
à partir des BDD de ses sous-formules.
Nous réalisons d'abord une fonction qui alloue et partage des
triplets A ¾® F';F'' comme des enregistrements
(``records'') en mémoire avec trois champs pour A, F' et
F'' respectivement. Pour ce faire, nous utilisons une table de
hachage globale (``hash-table'', cf. [Knu73]) qui
mémorise tous les triplets construits antérieurement. Les tables
de hachage sont faites de sorte que, étant donnés A, F',
F'', soit un triplet A¾®F';F'' est déjà
dans la table et on peut retourner son adresse rapidement, ou bien on
annonce son absence rapidement. Un algorithme simple de table de
hachage qui fonctionne bien en pratique consiste à fixer un entier
N suffisamment grand (et premier pour de meilleurs résultats), et
d'allouer un tableau global à N entrées, vides au départ. Ces
entrées contiendront des listes chaînées de triplets déjà
construits.
Pour découvrir si A ¾® F';F'' est dans la
table, nous calculons d'abord une fonction de hachage
h(A,F',F'') sur A, F', F'', qui retourne un entier
entre 0 et N-1 (i.e., un index dans la table). Comme tous les BDD
identiques sont partagés, ils sont décrits de façon unique par
leur adresse en mémoire : un bon choix pour h(A,F',F'') est
la somme des adresses de A, F' et F'', modulo N.
L'invariant de la table est que si A¾®F';F'' est
dans la table, il est dans la liste à l'entrée numéro i de la
table, où i=h(A,F',F'').
Pour trouver si A ¾® F';F'' est déjà dans la
table, alors, calculer i=h(A,F',F''); parcourir la liste dans
l'entrée i, et comparer chaque élément avec l'enregistrement
de composantes A, F' et F''. Si nous rencontrons le
triplet attendu, nous retournons son adresse. Sinon, nous
annonçons son absence. De même, pour allouer et partager
A¾®F';F'', nous le recherchons dans la table, et
le retournons si nous l'avons trouvé; sinon, nous allouons un nouvel
enregistrement contenant A, F', F'', le rajoutons en
tête de la liste à l'entrée numéro i, et retournons son
adresse.
Le temps moyen pour retrouver ou construire et partager un triplet
A¾®F';F'' est de l'ordre de n/N, où n est
le nombre de triplets antérieurement alloués. Si n n'est pas
plus large que N dans de trop grandes proportions, ceci est
quasi-instantané.
Pour construire des BDD, nous définissons d'abord la fonction
BDDmake comme suit : si F'=F'' (noter que nous
comparons les BDD par adresse et non récursivement par contenu,
puisqu'ils sont partagés), alors BDDmake(A,F',F'') retourne F'; sinon, BDDmake(A,F',F'') alloue et partage
A¾®F';F'' et retourne son adresse.
La négation BDDneg(F) d'un BDD F est définie
par récursion structurelle comme suit : BDDneg(T)=F,
BDDneg(F)=T, BDDneg(A¾®F+;F-)= BDDmake(A,BDDneg(F+),BDDneg(F-)). Si ° est un opérateur binaire
quelconque, nous définissons l'opération correspondante comme
suit. Prenons l'exemple de la disjonction, réalisée par la
fonction BDDor :
- BDDor(T,F)=T, BDDor(F,F)=F;
- BDDor(F,T)=T, BDDor(F,F)=F;
- si F=A¾®F+;F-, et
F'=A'¾®F'+;F'-, alors:
- si A<A', alors
BDDor(F,F')= BDDmake(A,BDDor(F+,F'), BDDor(F-,F'));
- si A>A', alors
BDDor(F,F')= BDDmake(A',BDDor(F,F'+), BDDor(F,F'-));
- si A=A', alors
BDDor(F,F')= BDDmake(A,BDDor(F+,F'+), BDDor(F-,F'-)).
Le seul problème si nous codons ces fonctions naïvement, est
qu'elles tournent en temps environ proportionnel au nombre de chemins dans le BDD, et non son nombre de noeuds. C'est
un point important, parce qu'à cause du partage, les BDD peuvent
avoir moins de noeuds qu'ils n'ont de chemins, et ce dans des
proportions astronomiques.
Nous codons donc BDDneg et BDDor en utilisant
des mémo-fonctions: une mémo-fonction est une fonction f
associée à une table de hachage T qui enregistre tous les
résultats précédemment calculés par f. Pour être plus
précis, T envoie des arguments de f vers les résultats
correspondants de f. La mémo-fonction consulte d'abord la table
de hachage T, et recherche une entrée correspondant à ses
arguments. Si elle en trouve une, elle retourne le résultat
enregistré. Sinon, elle appelle la fonction ordinaire f,
enregistre le couple (argument, résultat) dans la table T et
retourne le résultat. Cette astuce fait tourner BDDneg
et BDDor en temps quasi-linéaire et quasi-quadratique
respectivement.






 .
.
 correspond alors à ¾® .)
À partir de maintenant, clause voudra dire séquent,
écrit avec Ú et ¬ au lieu de la notation à flèche
précédente. C'est à strictement parler un abus de langage,
d'autant plus que les contractions (remplacer FÚF par
F) sont sous-entendues dans les clauses. Nous utilisons cette
notation parce qu'elle est traditionnelle, et parce qu'elle apporte
des intuitions sémantiques utiles.
correspond alors à ¾® .)
À partir de maintenant, clause voudra dire séquent,
écrit avec Ú et ¬ au lieu de la notation à flèche
précédente. C'est à strictement parler un abus de langage,
d'autant plus que les contractions (remplacer FÚF par
F) sont sous-entendues dans les clauses. Nous utilisons cette
notation parce qu'elle est traditionnelle, et parce qu'elle apporte
des intuitions sémantiques utiles.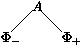
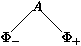 (Remarquer que la branche ``A vrai'' est à droite, alors que la
branche ``A faux'' est à gauche, ce qui est l'ordre inverse de
F+ et F-.)
(Remarquer que la branche ``A vrai'' est à droite, alors que la
branche ``A faux'' est à gauche, ce qui est l'ordre inverse de
F+ et F-.)




