Systèmes de Preuve

3 Systèmes de Preuve

Maintenant, c'est une chose d'avoir une sémantique pour la logique propositionnelle classique, mais elle est ardue à utiliser pour décider si une formule donnée F est valide ou non, satisfiable ou non. Bien qu'il soit possible d'énumérer toutes les affectations (restreintes aux variables libres de F), ceci peut demander un temps fabuleux. Le nombre d'affectations différentes à tester est en effet 2ⁿ, où n est le nombre de variables libres de F : c'est fini, mais devient rapidement trop large en pratique lorsque n devient grand.

Nous avons donc besoin d'autres façons d'exprimer les formules valides, resp. insatisfiables. L'une des plus intéressantes est d'examiner les preuves bien formées, et de considérer leurs conclusions, que l'on appelle les théorèmes. Ce faisant, nous espérons (en supposant pour l'instant que les théorèmes coincident avec les tautologies) que tous, ou au moins une grande proportion des théorèmes ont des preuves courtes, ou du moins des preuves qui soient plus petites qu'une table de vérité. Ceci a deux avantages : en premier, une preuve courte est préférable à une longue liste d'affectations comme explication de la validité de la formule considérée; et si un théorème a une preuve courte, alors elle sera plus facile à trouver, que ce soit à la main ou par une machine, que de tester toutes les affectations possibles.

Le pendant du langage des propositions en matière de preuve est un langage appelé système de preuve. Il en existe de nombreux, tous aussi expressifs, et nous en définissons quelques-uns dans cette section.

Une question immédiate vient à l'esprit : y a-t-il un rapport entre tautologies et théorèmes propositionnels ? Dans tous les systèmes de preuve que nous présenterons, les théorèmes seront précisément les tautologies, ce qui était le but recherché. Ceci se décompose en une preuve de correction (tous les théorèmes sont valides) et une de complétude (toutes les tautologies sont prouvables).

3.1 Systèmes de Hilbert

David Hilbert a été l'un des premiers mathématiciens à s'intéresser à la mécanisation des preuves et de la recherche de théorèmes. Les preuves en format de Hilbert sont des suites de propositions, qui sont des axiomes ou des conséquences de propositions précédentes, déduites par des règles de preuve bien définies.

Définition 11 Un système de preuve en format de Hilbert est un couple (A,R), où A est un ensemble de formules appelées les axiomes, et R est un ensemble de règles d'inférence ou règles de preuve, c'est-à-dire des relations entre ensembles de formules (les prémices) et des formules (la conclusion).

Une dérivation à partir d'un ensemble G d'hypothèses est une suite non vide F₁, F₂, ..., F_n, n>0, de formules telles que pour tout i entre 1 et n, F_i est un axiome (F_iÎA), ou un élément de G, ou est déduit des formules précédentes dans la suite (D r F_i, pour une certaine rÎR et un certain DÍ{F₁,...,F_i-1}).

Une preuve p d'une formule F à partir de G est une dérivation à partir de G dont la dernière formule est F. S'il existe une preuve de F à partir de G, nous disons que G prouve F, ou que F est prouvable à partir de G, et nous écrivons G|-⁽^A^,^R⁾F. Un théorème est une formule qui est prouvable à partir de l'ensemble d'hypothèses vide.

Si G et G' sont deux ensembles de formules, alors G,G' représente l'union de G et G'; si F est une formule, G,F et F,G représentent G È {F}; l'ensemble vide est représenté par une espace.

Un exemple classique de système de Hilbert pour la logique propositionnelle classique est le système SKC suivant. Ses axiomes sont :

(K) FÞF'ÞF,
(S) (FÞF'ÞF'') Þ(FÞF') Þ(FÞF''),
(C) ¬¬FÞF

pour toutes formules F, F' et F''. Sa seule règle d'inférence est le modus ponens :

(MP) de F et FÞF', deduire F', pour toutes F, F'.

Dans ce système, il est sous-entendu que Þ et F sont le seul connecteur et la seule constante logiques, respectivement. ¬ F est une abréviation de F Þ F, F Ù F' de ¬ (F Þ ¬ F'), F Ú F' de ¬ F Þ F'.

Théorème 12  [Correction]  Si G|-^SKCF, alors G|=F.
Preuve : Par récurrence sur la longueur d'une preuve de F à partir de G : exercice. ¤

Le fait que le système soit correct entraîne qu'il est cohérent:

Théorème 13  [Cohérence]   Le système SKC est absolument cohérent, c'est-à-dire qu'il existe une formule F que SKC ne peut pas prouver.

Le système SKC est cohérent par rapport à la négation, c'est-à-dire qu'il n'existe aucune formule F telle que F et ¬F soient toutes deux prouvables.
Preuve : Exercice. ¤

Théorème 14  [Complétude]   Si G|=F, alors G|-^SKCF.

Nous ne le démontrerons pas. Nous disons que SKC est complet par rapport à la sémantique de la logique classique propositionnelle. Il s'agit de la réciproque de la correction. Une conséquence importante (qu'il faut en fait démontrer d'abord pour pouvoir prouver la complétude) est que Þ est, comme nous nous en doutions, très lié à la notion de déductibilité :

Théorème 15  [Théorème de la déduction]   G,F|-^SKCF' si et seulement si G|-^SKCFÞF'.
Preuve : Utiliser la correction et la complétude (exercice). ¤

Une autre conséquence est la décidabilité de la logique propositionnelle :

Théorème 16  [Decidabilité]   Il existe un algorithme qui, étant donné un ensemble fini G de formules et une formule F, décide si G|-^SKCF.
Preuve : Décider G|-^SKCF signifie décider G|=F, par correction et complétude. De plus, nous pouvons supposer que G est vide sans perte de généralité, par le théorème de la déduction. Mais [F]r ne dépend que des valeurs que prend r sur les variables libres de F, par une récurrence structurelle aisée sur F : énumérer les restrictions des affectations à fv(F) (il n'y en a qu'un nombre fini), et évaluer F dans chaque. Ceci prend un temps fini. ¤

Bien sûr, énumérer toutes les affectations aux variables libres peut prendre beaucoup de temps. En fait, les systèmes de Hilbert ne donnent pas d'explication raisonnable de pourquoi une formule est valide : l'argument ci-dessus ne cherche pas réellement de preuve, et en fait les preuves en SKC sont extrêmement illisibles.

3.2 Déduction naturelle

Le principal défaut des systèmes de Hilbert est le fait que nous ne pouvons pas poser d'hypothèse auxiliaire. Pour prouver F Þ F', il n'y a pas de mécanisme nous permettant de poser F en hypothèse pour en déduire F'. (Quoique le théorème de la déduction nous affirme que ce serait correct de le faire.)

Les systèmes de déduction naturelle corrigent cette situation, et peuvent être présentés sous des formats différents, tous équivalents.

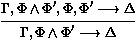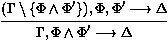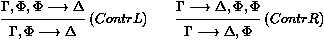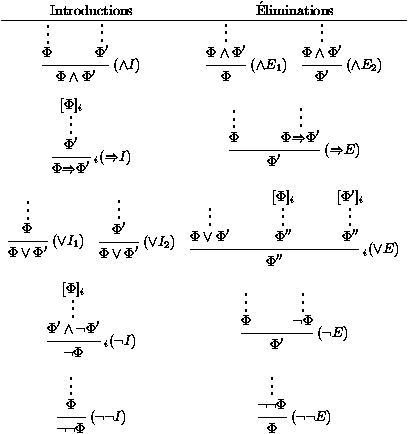
Figure 1: Déduction naturelle

Une première façon de présenter les systèmes de déduction naturelle est de dire que les preuves sont des diagrammes bi-dimensionnels de formules connectées par des règles de preuve. Ces règles, pour la logique classique propositionnelle, sont classées en règles d'introduction et règles d'élimination (figure 1). Trois petits points verticaux (:) abrègent un arbre de dérivation entier. Les règles combinent des arbres de dérivation pour en produire de nouveaux.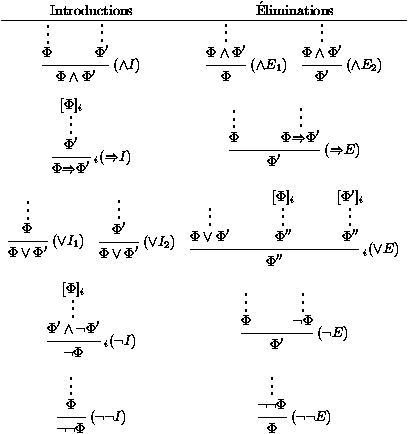

Par exemple, si (p) est une dérivation qui prouve F, et (p') est une déerivation qui prouve F', alors la dérivation suivante prouve FÙF' :

(Ù I) est la règle d'introduction du connecteur de conjonction. De deux preuves de deux formules, elle construit une preuve de la conjonction. De façon symétrique, (Ù E₁) et (Ù E₂) prennent une dérivation d'une conjonction, et retournent une des sous-formules sous le connecteur Ù : ces règles éliminent donc un signe Ù de la formule.

La règle (¬ E) a comme conclusion une formule arbitraire F' : de F et ¬ F, une contradiction, nous pouvons en effet déduire n'importe quoi.

Les autres règles s'expliquent d'elles-mêmes, sauf celles qui utilisent la notation [ ]_i : (Þ I), (¬ I) et (Ú E). Les crochets représentent une hypothèse qui a été déchargée. Regardons par exemple la règle (Þ I). Elle dit que si (p) est une preuve de F' utilisant F comme hypothèse, soit si :

alors nous pouvons déduire de cette preuve une de FÞF' sans utiliser F comme hypothèse auxiliaire, de sorte que nous pouvons barrer F --- la décharger --- et ajouter une nouvelle ligne sous la preuve. La notation utilisée pour décharger F est [F]_i, où i est une étiquette unique (disons un entier) dont nous nous servons pour associer l'inférence de FÞF' avec les occurrences de F que nous déchargeons. Déchargeons F ci-dessus :

La format bi-dimensionnel est difficile à étudier métamathématiquement, car l'identification des hypothèses auxiliaires n'est pas claire : dans une dérivation d'une formule, nous devons parcourir toute la dérivation pour chercher les hypothèses non déchargées.

Figure 2: Déduction naturelle en format de séquents

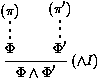
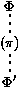
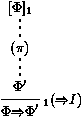
Une présentation plus formelle de la déduction naturelle qui montre à la fois les formules et l'ensemble des hypothèses auxiliaires, est la déduction naturelle en format de séquents. Au lieu de dériver juste des formules F, nous dérivons des séquents G¾®F, où G est un ensemble de formules, appelé le contexte du séquent. Il s'agit précisément de l'ensemble des hypothèses auxiliaires courantes alors que nous cherchons à prouver F. Les règles de preuve sont données en figure 2, où F est n'importe quelle formule insatisfiable, par exemple F'Ù¬F'. Remarquer à quel point les manipulations de contextes sont moins complexes qu'avec la notation [ ]_i, puisque les hypothèses auxiliaires sont décrites explicitement dans chaque séquent.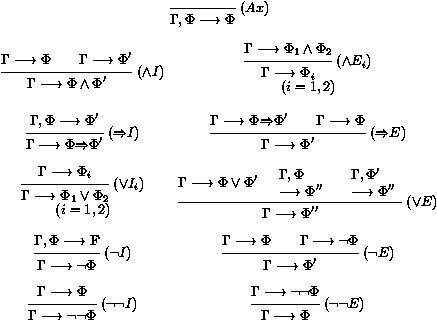

Définition 17  Une dérivation en déduction naturelle est un arbre inversé dont les noeuds sont des séquents connectés par des règles de déduction de la figure 2. Les feuilles sont des instances de la règle (Ax) et sont appelées des axiomes.

Une preuve p d'un séquent G¾®F est une dérivation en déduction naturelle dont la racine est décorée par G¾®F. Nous disons aussi que p est une preuve de F à partir de G. S'il existe une preuve de G¾®F, nous disons que G¾®F est prouvable, ou bien que F est prouvable à partir de G, et nous écrivons |-^NDG¾®F, ou G|-^NDF.

Un théorème est une formule prouvable à partir de l'ensemble d'hypothèses vide.

Le théorème de la déduction (G,F |-^ND F' si et seulement si G |-^ND F Þ F') est évident dans ce formalisme. Noter aussi que la règle (Þ E) est précisément la règle (MP) de la section 3.1.

Théorème 18  [Correction]  Si G|-^NDF, alors G|=F.
Preuve : Exercice. ¤

Théorème 19  [Complétude]   Si G|=F, alors G|-^NDF.
Comme plus haut, nous ne prouverons pas ce théorème.

Théorème 20  [Decidabilité]   Il existe un algorithme qui, étant donné un ensemble fini G de formules et une formule F, décide si G|-^NDF.
Preuve : L'algorithme teste si G|=F, comme au théorème 16. Il est encore une fois difficile trouver une preuve directement. ¤

3.3 Séquents de Gentzen

Bien que la déduction naturelle soit plus commode que les systèmes de Hilbert pour écrire des preuves, il est encore malaisé de chercher une preuve d'une proposition donnée, à part en testant indirectement si elle est valide. Gerhard Gentzen a inventé ce que nous appelons maintenant des systèmes de séquents pour représenter les preuves en logique classique. Nous définissons maintenant la version propositionnelle du système LK₀ de Gentzen.

Définition 21 Un séquent de Gentzen est un couple G, D d'ensembles finis de formules, noté G¾®D.

Nous autorisons donc plusieurs formules, ou même aucune formule, à la droite d'un séquent. Ceci rend le calcul symétrique, en particulier, et nous permettra d'éviter les détours qu'il fallait parfois prendre pour prouver certaines formules en déduction naturelle.

Figure 3: Le système LK₀ de Gentzen

En ce qui concerne la sémantique, G¾®D signifie que la conjonction des formules de G entraîne la disjonction des formules de D, c'est-à-dire qu'une formule de D est vraie dès que toutes les formules de G sont vraies.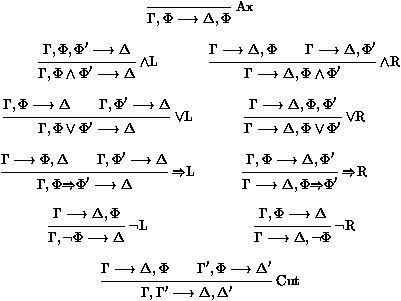

Alors LK₀ est le système de preuve défini par les règles de la figure 3, où G, G', D et D' sont des ensembles finis de formules et F, F' sont des formules. Nous y trouvons l'axiome Ax, comme en déduction naturelle, des règles à gauche (L) et à droite (R) pour chaque connecteur, et la règle spéciale de coupure Cut. Les coupures sont des applications de lemmes : d'une preuve de F (en disjonction avec D) dans le contexte G, et d'une preuve d'un lemme établissant que si F est vraie, alors D' est une conséquence de G', nous obtenons une preuve de D' (en disjonction avec D) dans le contexte G,G'.

Définition 22  Soit G¾®D un séquent de Gentzen, et r une affectation. Nous disons que r satisfait G ¾® D, ce que nous notons r |= G ¾® D, si et seulement s'il existe une formule F dans D telle que r |= F, ou une formule F dans G telle que non r |= F.

Nous disons que G¾®D est prouvable dans LK₀ si et seulement s'il existe une dérivation dans LK₀ se terminant sur G ¾® D. Nous écrivons alors |-^LK^₀ G ¾® D, ou G |-^LK^₀ D.

Théorème 23  [Correction]   Si |-^LK^₀G¾®D, alors |=G¾®D.
Preuve : Exercice. ¤

Théorème 24  [Complétude]   Si |= G ¾® D, alors |-^LK^₀ G ¾® D.

De plus, si c'est le cas, alors nous pouvons en trouver une preuve dans LK₀ qui n'utilise pas la règle Cut (une preuve sans coupure).
Preuve : Soit S l'ensemble des séquents G' ¾® D' tels que G' Ç D'=Ø et G' È D' Ë X, et soit f une application associant à chaque séquent G' ¾® D' dans S une formule non variable dans G' + D', où + représente la somme directe. On appellera f la stratégie.

Construisons l'arbre T dont la racine est G ¾® D, et dont les noeuds sont des séquents, récursivement comme suit. Si G' ¾® D' n'est pas dans S, nous disons que G' ¾® D' est une feuille de l'arbre. Sinon, soit F = f(G' ¾® D'). Alors les fils de G' ¾® D' sont les prémices de la règle dont la conclusion est G' ¾® D', portant sur F.

Plus formellement, soit FÎG' soit FÎD'. Si FÎG', soit G'' = G'\{F}, et définissons les fils de G' ¾® D' comme étant G'' ¾® F',D' si F est de la forme ¬F'; G'',F',F'' ¾® D' si F vaut F'ÙF''; G'',F' ¾® D' et G'',F'' ¾® D' si F vaut F'ÚF''; G'' ¾® F',D' et G'',F'' ¾® D' si F vaut F'ÞF''. D'autre part, si FÎD', soit D'' = D'\{F}, et définissons les fils de G' ¾® D' comme G',F' ¾® D'' si F vaut ¬F'; G' ¾® F',D'' et G' ¾® F'',D'' si F vaut F'ÙF''; G' ¾® F',F'',D'' si F vaut F'ÚF''; G',F' ¾® F'',D'' si F vaut F'ÞF''. Remarquer que cet arbre est presque une preuve sans coupure dans LK₀; en effet, les huit conditions définissant les fils des noeuds autres que des feuilles sont respectivement ¬L, ÙL, ÚL, ÞL, ¬R, ÙR, ÚR, ÞR. (Tracer l'arbre la racine en bas pour voir qu'il ressemble réellement à une preuve dans LK₀.) Pour montrer que T est réellement une preuve, nous devons vérifier que T est un arbre fini, et que ses feuilles sont prouvables dans LK₀, par la règle Ax. Montrons que T est un arbre fini. Définissons la longueur d'une formule comme suit : la longueur d'une variable propositionnelle est 1, la longueur de ¬F' est un plus la longueur de F', la longueur de F'°F'' est un plus la longueur F' plus celle de F', pour tout connecteur binaire °. Par récurrence sur la somme L des longueurs des formules dans G,D, nous voyons que la profondeur de T ne dépasse pas L, et donc que le nombre de noeuds dans T ne dépasse pas 2^L. Nous montrons maintenant que les feuilles sont des instances de la règle Ax. Par construction, un noeud qui n'est pas une feuille de T est valide (en tant que séquent) si et seulement si ses fils sont valides. Par récurrence structurelle sur T, nous concluons que toutes ses feuilles sont des séquents valides. Mais si G' ¾® D' est une feuille, par définition G' Ç D' ¹ Ø (donc c'est une instance de Ax), ou bien G' et D' ne contiennent que des variables propositionnelles. Dans ce dernier cas, si nous avions G' Ç D'=Ø, nous pourrions définir une affectation r en associant T à chaque variable de G', et F à chaque variable de D', ce qui contredirait le fait que G' ¾® D' est valide. Dans tous les cas, les feuilles sont des instances de Ax. Ceci termine la preuve. ¤

Ce théorème montre non seulement que LK₀ est complet, mais en plus que nous n'avons pas besoin de la règle Cut : si une proposition est prouvable, on peut aussi la prouver sans aucun lemme intermédiaire.

Une preuve sans coupure peut être beaucoup plus grosse qu'une preuve avec des coupures. L'intérêt principale de l'élimination des coupures en démonstration automatique, cependant, est que l'espace de recherche des preuves sans coupure est localement plus petit que l'espace de toutes les preuves : si nous cherchons à construire une preuve sans coupure de bas en haut, à chaque étape nous choisissons une formule non variable arbitraire dans le séquent courant, disons F Ù F' à gauche, et nous savons immédiatement quelle règle utiliser (ici, ÙL) et quelles formules apparaîtront dans les prémices (F et F' ici). Ce ne serait pas le cas en présence de Cut, qui doit inventer une formule arbitraire F lors de la remontée de la conclusion vers les prémices. Ceci est formalisé par le résultat suivant :

Lemme 25  [Propriété de la sous-formule]  Dans une preuve sans coupure de G ¾® D, tous les séquents sont composés de sous-formules des formules de G,D uniquement.
Preuve : Exercice. ¤

En fait, nous avons prouvé plus : nous n'avons même pas besoin de contraction. Expliquons-nous. Voici une instance légitime de ÙL:

Il s'agit en effet de la règle de la figure 3, avec G, FÙ F' au lieu de G, parce que FÙ F', F Ù F' n'est rien d'autre que F Ù F' (l'union ensembliste est idempotente). Mais nous aimerions chercher une preuve sans coupure en remontant à partir du but. Une instance comme ci-dessus de ÙL peut être appliquée infiniment longtemps. Le théorème 24 montre que nous n'avons en fait jamais besoin de telles instances, autrement dit nous pouvons nous restreindre à n'utiliser que le cas particulier suivant de ÙL :

et de même pour les autres règles.

Une façon plus formelle de traiter ce problème est d'utiliser des séquents G ¾® D, où G et D ne sont plus des ensembles mais des multi-ensembles, c'est-à-dire des ensembles d'éléments comptés avec leurs multiplicités, ou de façon équivalente des listes où l'ordre des éléments n'a aucune importance. Les règles de LK₀ sont alors encore celles de la figure 3, mais où la virgule dénote l'union des multi-ensembles, plus les règles de contraction :

Les arguments du théorème 24 montrent alors que tout séquent valide a une preuve aussi bien sans coupure que sans contraction.

Le fait que nous puissions limiter la recherche aux preuves sans coupure et sans contraction rend l'espace de recherche beaucoup plus petit que l'espace de toutes les preuves : il n'y a qu'un nombre fini de preuves sans coupure ni contraction, alors qu'il y a une infinité de preuves (même sans coupure). En fait, étant donné une stratégie f, il n'y a qu'une preuve sans coupure ni contraction obéissant à la stratégie. La réalisation habituelle de ces algorithmes est connue sous le nom de méthode des tableaux (cf. section 4.1).

Le fait que LK₀ est complet même sans la coupure peut être renforcé dans une autre direction :

Théorème 26 [Élimination des coupures] Il existe un algorithme qui prend une preuve dans LK₀, et la transforme en une preuve sans coupure du même séquent.

Nous ne fournissons pas (encore) la preuve. Ceci dit que traduire une preuve en une preuve sans coupure du même théorème est un processus effectif (on peut le programmer sur une machine). Intuitivement, les coupures nous permettent de réutiliser des lemmes prouvés antérieurement. Si, au lieu d'utiliser ces lemmes, nous rejouons leurs preuves, nous aboutissons à une preuve sans aucun lemme intermédiaire, c'est-à-dire sans coupure. La difficulté est de montrer que ce processus termine. Ceci a des conséquences importantes dans le domaine de la conception de langages de programmation, connues sous le nom de correspondance de Curry-Howard entre preuves et programmes, et entre formules et types.