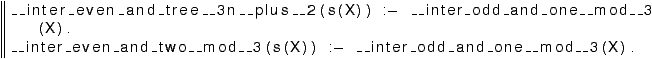3 The h1 Tool Suite through Examples

3 The `h1` Tool Suite through Examples

The h1 prover is the core of the h1 tool suite, and we shall explain the tool suite by running h1 on several examples.

The h1 prover is invoked by calling h1 with a sequence of flags, ended by a file name. The file name should contain a set of clauses in TPTP clause format. Such files conventionally end with the .p extension—but there is no obligation. Also, giving a single dash - as file name forces h1 to read the input clause set from standard input.

3.1 A Toy, Introductory Example

Examples are given in the distribution package. Here is a very small one (file test1.p):

This contains three clauses. Each clause is introduced by the keyword input_clause. The first argument, clause1, clause2, or clause3 above, is the name of the clause. Names are used in sundry ways, mainly for explanation and documentation purposes. It is good practice to give each clause a different name, but the tools of the h1 tool suite should work even when several clauses have the same name.

The second argument can be the keyword conjecture or axiom; h1 just does not care: write what you prefer here.

Finally, the third argument, enclosed between square brackets, is the clause itself. It is a list of literals, separated by commas. Each literal starts with a sign, ++ for positive literals, -- for negative literals. The clauses above are, in a more traditional notation:

	p(a)
	¬ p (X) `or` p (f (X))
	¬ p (f (f (X)))

This example is in fact a set of Horn clauses, which would be written in Prolog notation:

p (a)
p (f (X))	:-	p (X)
`false`	:-	p (f (f (X)))

Launch h1 on this file, test1.p, by typing

h1 test1.p

You will get the answer

*** Derived: clause3 ***

which means that a contradiction was found, using the clause named clause3 in the last step. In other words, in the present example, it says that a fact of the form p (f (f (t))), matching the body of clause3, can be deduced from the definite clauses (here, clause1 and clause2)

So far, so good, this is typically the least you could expect from a theorem prover.

However, h1 also produced two more files, test1.log and test1.model.pl. If you're curious, look at test1.log, by running

less test1.log

Oh well, it is long, but it is not meant to be read by a human reader! If you're perspicuous enough, you'll find some meaning buried inside this. However, this is really meant as a log file, from which h1trace can extract a (mostly) readable proof (Section 5), and which h1mc can use to get some essential information it needs (Section 6).

3.2 The Dreadsbury Mansion Murder Mystery Example

Here is a more complicated example, due to Len Schubert. This is problem 55 of [1986 (Pelletier)].

Someone in Dreadsbury Mansion killed Aunt Agatha. Agatha, the butler, and Charles live in Dreadsbury Mansion, and are the only ones to live there. A killer always hates, and is no richer than his victim. Charles hates noone that Agatha hates. Agatha hates everybody except the butler. The butler hates everyone not richer than Aunt Agatha. The butler hates everyone whom Agatha hates. Noone hates everyone. Who killed Agatha?

The problem is formalized in file butler-puzzle.p. The clauses are as follows. First, “Agatha, the butler, and Charles live in Dreadsbury Mansion, and are the only ones to live there.”:

`agatha_in_mansion`	`in_mansion` (agatha)
`charles_in_mansion`	`in_mansion` (charles)
`butler_in_mansion`	`in_mansion` (butler)

Then, “A killer always hates, and is no richer than his victim.”, that is, if X killed Y, then it must be the case that X hates Y, and on the other hand that X is not richer than Y:

`killer_hates_victim`	`hates` (X,Y)	:-	`killed` (X,Y)
`killer_no_richer`	`not_richer` (X,Y)	:-	`killed` (X,Y)

Next, “Charles hates noone that Agatha hates.” In other words, it is impossible that Charles and Agatha hate the same person X:

charles_hates_noone_agatha_hates false :- hates (charles,X), hates (agatha,X)

To write “Agatha hates everybody except the butler.”, we just say that Agatha hates herself and Charles:

`Agatha_hates_herself`	`hates` (agatha, agatha)
`Agatha_hates_charles`	`hates` (agatha, charles)

Now, “The butler hates everyone not richer than Aunt Agatha.”:

butler_hates_everyone_not_richer_than_agatha hates (butler, X) :- not_richer (X, agatha)

Then, “The butler hates everyone whom Agatha hates.”:

butler_hates_everybody_agatha_hates hates (butler, X) :- hates (agatha, X)

Next, “Noone hates everyone.”, which we formulate as “noone hates Agatha, Charles, and the butler”:

noone_hates_everyone false :- hates (X,agatha), hates (X,butler), hates (X, charles)

Finally, we explore who may have killed Aunt Agatha. To do this, we shall enumerate the potential murderers, and use the C preprocessor cpp to replace the macro identifier WHO in the following clause by each resident of Dreadsbury Mansion:

WHO_killed_agatha killed (WHO, agatha)

Let us test whether the butler killed Agatha. Run butler-puzzle.p through cpp with WHO equal to butler, and feed the output to h1; h1 reads from standard input when given - as file name:

cpp -P -DWHO=butler butler-puzzle.p | h1 -

You get the output:

*** Derived: noone_hates_everyone ***

In other words, the butler cannot have killed Agatha (contrarily to proper conventions in popular whodunnit mysteries), because this would contradict the fact that noone hates everyone.

More information can be gotten from the trace file h1out.log. (Running h1 on file <file>.p produces a trace file <file>.log. If no input file is given, as here, the trace file is called h1out.log.) We shall explain how to use this trace file in Section 5. For now, just run

h1trace h1out.log >dummy

and open the file dummy. You'll see that the first lines say:

. #false(noone_hates_everyone) [noone_hates_everyone]. using assumption #false(noone_hates_everyone) :- hates(X1,charles), hates(X1,butler), hates(X1,agatha). {X1=butler}

In other words, assuming the butler killed Agatha would involve that the butler hates everyone, which is impossible. The rest of file dummy is a tree-like proof that indeed the butler hates everyone, i.e., hates Agatha, Charles, and himself in this case.

So did Charles kill Agatha instead?

cpp -P -DWHO=charles butler-puzzle.p | h1 -

No, this would contradict the fact that Charles hates noone that Agatha hates. In this case, Charles hates Agatha, and Agatha hates herself, whence the contradiction.

*** Derived: charles_hates_noone_agatha_hates ***

There is only one possibility remaining: that Agatha killed herself.

cpp -P -DWHO=agatha butler-puzzle.p | h1 -

and indeed, h1 does not complain: assuming Agatha killed herself leads to no contradiction. The file h1out.model.pl describes the least model of this clause set.

This could have been found automatically by a simple sh script, listing all possible murderers of Aunt Agatha.

for who in butler charles agatha
do
  if (cpp -P -DWHO=$who butler-puzzle.p | h1 - 2>&1\
                                        | grep -q Derived)
  then echo $who did not kill agatha.
  else echo $who may have killed agatha.
  fi
done

Since somebody killed Agatha, it must be herself.

butler did not kill agatha. charles did not kill agatha. agatha may have killed agatha.

The point of this example is that, first, the clauses are clearly not (alternating tree) automata clauses; and second, that they are H₁ clauses. Check this by running h1 with the -check-h1 2 option:

cpp -P -DWHO=agatha butler-puzzle.p | h1 -check-h1 2 -

This makes h1 run as above, except it would have failed if any of the input clauses where not in H₁. By default, h1 runs as h1 -check-h1 0, which does not check anything, but computes an approximation, see Section 3.4.

That the clauses of butler-puzzle.p are in the H₁ class may seem surprising. After all, H₁ clauses are required to use only unary predicates, i.e., all predicate letters P can only take one argument. This is certainly not the case of the hates, killed, and not_richer predicates above, which are all binary!

The trick here is that, when h1 sees an n-ary predicate P (t₁, …, t_n) in its input, it converts it first to P (f_P (t₁, …, t_n)) for some fresh n-ary function symbol f_P. (Different occurrences of P correspond to the same symbol f_P.) This makes P unary, and does not change the semantics of clauses in any essential way. Under the hood, h1 typically builds f_P by prepending a sharp sign # in front of the name of P, guaranteeing that no clash occurs with any function symbol you may have used. Don't count on it, though, as this may change in future releases. Also, the h1 tools try to hide this kludge as much as they can, and will happily parse and print n-ary predicate symbols.

We shall return to this example in Section 3.3.8.

3.3 Computing with Tree Automata

Assume that we wish to compute the intersection of the languages L₁ of all lists of even natural numbers, and L₂ of all trees with binary nodes labeled with cons, and whose leaves are either nil or natural numbers of the form 3n+2, n in |N.

We have already seen what an automaton recognizing L₁ looked like, see Figure 1. In TPTP format, this is file listeven.p:

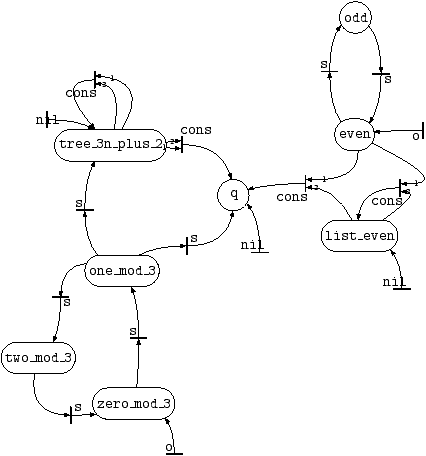
The language L₂ is described by the predicate (final state) tree_3n_plus_2. Look at file tree3plus2.p:

By the way, we can convert any automaton in TPTP format into Prolog format by running h1 with the -no-trim option:

h1 -no-trim tree3plus2.p

Normally, h1's default is to use the -trim option, which trims away all clauses that are obviously not needed for deriving a contradiction. (See Section 4.1 for more information on -trim and -no-trim.) In this case, trimming would just eliminate all clauses! Since we are not looking for a contradiction, we just run h1 without trimming, and get a model in tree3plus2.model.pl:

In other words, h1 can be used to convert any set of H₁ clauses into an equivalent alternating tree automaton by running it with the -no-trim option and looking into the generated model file, ending in .model.pl.

3.3.1 Visualizing Tree Automata

Before we compute the intersection of L₁ and L₂, let us visualize the automaton defining L₂. This is accomplished using pl2gastex, see Figure 2. For more information on pl2gastex, and how to read such pictures precisely, see Section 13.

Figure 2: Trees with leaves equal to nil or to 3n+2, n in |N

3.3.2 Computing Intersections of Tree Automata

Now compute the intersection. Build a file, say list_even_inter_tree3plus2.p, by concatenating the clauses from listeven.p and from tree3plus2.p, and add the so-called intersection clause

q (X) :- list_even (X), tree_3n_plus_2 (X)

meaning that q holds of all terms that are both lists of even numbers, and trees as recognized at tree_3n_plus_2. Just run the following commands:

OUT=list_even_inter_tree3plus2
cat listeven.p tree3plus2.p >$OUT.p
echo "input_clause ($OUT, axiom, \
        [++q(X), --list_even(X),\
        --tree_3n_plus_2(X)])" >>$OUT.p

Because of the intersection clause above, the resulting clause set is not an alternating tree automaton as we have defined it. However, run h1 -no-trim on it:

h1 -no-trim list_even_inter_tree3plus2.p

and look at the generated alternating tree automaton. This is obtained, as usual, in a file named list_even_inter_tree3plus2.model.pl:

Graphically, this is the alternating tree automaton of Figure 3.

Figure 3: Trees with leaves equal to nil or to 3n+2, which are lists of even natural numbers at the same time

Note the presence of new nodes labeled ∧ in Figure 3. They represent intersections of languages. Indeed, there are two ways one can construct an element of q. First, there is nil. Second, there are terms of the form cons applied to two arguments X₁ and X₂, where X₁ is recognized both at tree_3n_plus_2 and at even, and X₂ is recognized both at tree_3n_plus_2 and at list_even.

The alternating tree automaton above recognizes (at q) the terms in the intersection of L₁ and L₂. One should observe that computing intersections of two languages by concatenating the clause sets defining each and adding an intersection clause is rather cavalier. It is only correct here because the two files listeven.p and tree3plus2.p share no predicate symbol. In general, one might allow shared predicate symbols, provided they have the same semantics in each file. For example, it is legal for the two files to both use the predicate even provided it denotes the set of even natural numbers in both. Otherwise, strange things may happen (an over-approximation will be computed).

3.3.3 Checking Tree Automata for Emptiness, Testing Membership

It may not be completely obvious whether such an alternating tree automaton is empty or not. (To say the least. The problem is DEXPTIME-complete.) Let us see whether the intersection state q is empty or not. In general, given a satisfiable set S of Horn clauses (e.g., definite clauses, in particular alternating tree automata clauses), the language of terms recognized at state P in S is empty if and only if S plus the clause false :- P (X) is satisfiable. Running:

(cat list_even_inter_tree3plus2.p;\
 echo "input_clause(q_is_not_empty, conjecture, [--q(X)]).")\
  | h1 -log-out - >list_even_inter_tree3plus2.log

yields

*** Derived: q_is_not_empty ***

meaning that there are indeed terms recognized at state q in the intersection.

We have kept a trace of the derivation in the log file list\_even\_inter\_tree3plus2.log. We can then use h1trace to get a mostly readable proof of the fact that q is non-empty; in particular, to have an example of a term recognized at q:

%-*-mode:outline;outline-regexp:"[0-9a-z.]+"-*-
. #false(q_is_not_empty).
  using assumption #false(q_is_not_empty) :- q(X1).
   {X1=nil}
1. q(nil).
    using assumption q(X1) :- tree_3n_plus_2(X1), list_even(X1).
     {X1=nil}
1.1. tree_3n_plus_2(nil) by assumption.
1.2. list_even(nil) by assumption.

In fact, the empty list nil is recognized at q ({X1=nil} at line 4 above). How to read such proofs will be explained in Section 5.

Let us test membership of some ground term. Is the list cons (s (s (o)), nil) consisting of just the natural number 2 in the intersection? In general, given S as above, a ground term t is recognized at state P if and only if S plus the clause false :- P (t) is satisfiable.

(cat list_even_inter_tree3plus2.p;\
 echo "input_clause(q_rec_cons_2_nil, conjecture,\
         [--q(cons(s(s(o)),nil))]).")\
  | h1 -

yields

*** Derived: q_rec_cons_2_nil ***

So cons (s (s (o)), nil) is in the intersection.

On the other hand, the list cons (s (s (s (s (o)))), nil) containing just the natural number 4 is not in the intersection. Run

(cat list_even_inter_tree3plus2.p;\
 echo "input_clause(q_rec_cons_4_nil, conjecture,\
         [--q(cons(s(s(s(s(o)))),nil))]).")\
  | h1 -

and you'll get (no message at all). Indeed, cons (s (s (s (s (o)))), nil) is a list of even natural numbers, but not a tree whose numeric leaves are of the form 3n+2, n in |N.

We can do more this way. Is there a term of the form cons (s (X), X), with the same X, in the intersection? Run

(cat list_even_inter_tree3plus2.p;\
 echo "input_clause(q_rec_cons_sX_X, conjecture,\
         [--q(cons(s(X),X))])") \
  | h1 -

and you'll get (no message at all). So there is none.

Is there a list whose first element is at least 3 in the intersection? Run

(cat list_even_inter_tree3plus2.p;\
 echo "input_clause(q_rec_cons_sssX_Y, conjecture,\
         [--q(cons(s(s(s(X))),Y))])") \
  | h1 -

and you'll get

*** Derived: q_rec_cons_sssX_Y ***

So there is one. We don't know which. However, we may use h1trace as above to have an idea (left as an exercise!).

Another possibility to have an idea of which lists whose first element is at least 3 in the intersection is to build the automaton recognizing all solutions, by running

(cat list_even_inter_tree3plus2.p;\
 echo "input_clause(what_q_rec_cons_sssX_Y, conjecture,\
         [++r(X,Y), --q(cons(s(s(s(X))),Y))])") \
  | h1 -no-trim -
mv h1out.model.pl rinter.model.pl

The resulting automaton, in file rinter.model.pl, is:

And graphically, this is the automaton of Figure 4.

Figure 4: Lists starting with a number at least 3 as recognized in state q of Figure 3

3.3.4 Converting Alternating to Non-Deterministic Tree Automata

All right, this starts being a tad intricate. In general, alternating tree automata are not that easy to read. We may eliminate intersection nodes ∧, and get a non-deterministic tree automaton instead by using the -no-alternation option to h1. Either use

h1 -no-trim -no-alternation

instead of h1 -no-trim (this will produce a non-deterministic, i.e., not an alternating tree automaton, in rinter.model.pl), or simply run

h1 -no-trim -model

on rinter.model.pl to eliminate intersection nodes. Just as

h1 -no-trim

can be used to conv ert an H₁ clause set into an equivalent alternating tree automaton,

h1 -no-trim -no-alternation

converts an H₁ clause set, or an alternating tree automaton, into an equivalent non-deterministic tree automaton. Run

pl2tptp rinter.model.pl >rinter_nd.p
h1 -no-trim -no-alternation rinter_nd.p

This yields the following automaton in file rinter_nd.model.pl.

Using pl2gastex on the output rinter_nd.model.pl, we arrive at the non-deterministic tree automaton of Figure 5. This should be more readable. The final state is q. Note that the result still contains two copies of the automata recognizing respectively all lists of even numbers, and all trees with leaves of the form nil or 3n+2, which are not needed any longer.

Figure 5: Eliminating intersection nodes from Figure 4

The automaton of Figure 5, i.e., in file rinter_nd.model.pl, uses new states such as __inter_even_and_one__mod__3 (which recognizes all terms which are both even numbers and numbers of the form 3n+1). In general, these new states are named

__inter_P₁_P₂_…_P_n

and are meant to recognize all terms that are recognized at P₁ and at P₂ and ... and at P_n at the same time. They appear as P₁ ∩ P₂ ∩ … ∩ P_n under pl2gastex.

3.3.5 Purging Tree Automata

Well, Figure 5 should be more readable... but there is some junk here. First, there are two sub-automata, disconnected from the rest, defining the predicates zero_mod_3, one_mod_3, two_mod_3, tree_3n_plus_2, and odd, even, list_even. They do not contribute at all to the definition of the language of r. Second, there are also spurious states such as q, or __aux_1 (drawn as a small state

). Use plpurge to purge the automaton of Figure 5 from all spurious states, by running

plpurge -final r rinter_nd.model.pl >rinter_nd.purged.pl

Figure 6: Purging the automaton of Figure 5

Hence we see that the relation r is simply the relation relating all numbers that are both odd and equal to 2 modulo 3 (state odd ∩ two_mod_3) to all objects that are both lists of even numbers and trees of with leaves equal to nil or 3n+2 (state list_even ∩ tree_3n_plus_2).

Looking a bit more in depth, the numbers that are both odd and equal to 2 modulo 3 are 5, 11, 17, ..., in other words the numbers that are equal to 5 modulo 6. And the objects that are both lists of even numbers and trees of with leaves equal to nil or 3n+2 are just lists of numbers equal to 2 modulo 6.

3.3.6 Determinizing Tree Automata

Looking at Figure 6, we realize that taking the successor, i.e., applying the s function to a term recognized at odd ∩ one_mod_3, yields a term that is recognized both at even ∩ two_mod_3 and at even ∩ tree_3n_plus_2. This is a form of non-determinism: we may want to travel to either state, not knowing which will eventually lead to acceptance.

To cater for this, we may determinize our tree automata. This produces an equivalent deterministic tree automaton, i.e., a set of Horn clauses of the form

P (f (X₁, …, X_n))

P₁ (X₁), …, P_n (X_n)

(5)

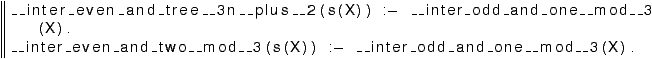
where X₁, ..., X_n are pairwise distinct variables, and where there is at most one such clause for each (n+1)-tuple (f, P₁, …, P_n). The automaton of Figure 6 is not deterministic because it contains the two clauses

By definition, a deterministic tree automaton can also be seen as a partial function I_f from tuples of predicates to predicates, one for each f. I.e., I_f (P₁, …, P_n) = P if there is a, necessarily unique, clause of the form (5).

To determinize the automaton rinter_nd.purged.pl of Figure 6, run

pldet rinter_nd.purged.pl >rinter_d.xml

This produces a deterministic tree automaton in file rinter_d.xml:

The format will be explained in more detail in Section 7.

We can then convert this deterministic tree automaton into Prolog notation, since every deterministic tree automaton is a particular case of a non-deterministic tree automaton (itself a particular case of an alternating tree automaton). Use auto2pl this way:

auto2pl rinter_d.xml >rinter_d.pl

This produces a file rinter\_d.pl, which is probably slightly more readable than the XML file above:

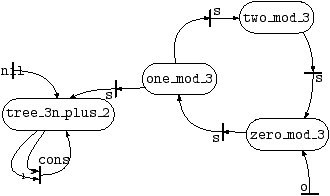
Now draw the resulting automaton in Figure 7, using pl2gastex:

pl2gastex rinter_d.pl >rinterd.tex

Figure 7: Determinizing the automaton of Figure 6

The automaton of Figure 7 is not too big. But beware: determinizing tree automata may produce automata that are exponentially larger in the general case. In fact, pldet may just take forever on some alternating, or even non-deterministic tree automata.

3.3.7 Computing Unions, Transitive Closures

We have seen how to compute intersections of tree automata in Section 3.3.2. Computing unions is just as easy. Say that you want to compute the union of the sets of lists of even numbers (listeven.p) and of the trees whose leaves are nil or 3n+2, n in |N. That is, instead of computing the intersection of the languages L₁ and L₂ introduced at the beginning of Section 3.3, we compute their union. As before, build a file, say list_even_union_tree3plus2.p, by concatenating the clauses from listeven.p and from tree3plus2.p, but this time add the two clauses

q (X)	:-	`list_even` (X)
q (X)	:-	`tree_3n_plus_2` (X)

so that the fresh state q recognizes the terms that are recognized by either the state list_even or by tree_3n_plus_2. Concretely, run the following commands:

OUT=list_even_union_tree3plus2
cat listeven.p tree3plus2.p >$OUT.p
echo "input_clause ("$OUT"_1, axiom, \
        [++q(X), --list_even(X)])." >>$OUT.p
echo "input_clause ("$OUT"_2, axiom, \
        [++q(X), --tree_3n_plus_2(X)])" >>$OUT.p

Now run h1 -no-trim as above:

h1 -no-trim list_even_union_tree3plus2.p

We get an equivalent alternating tree automaton in the file list_even_union_tree3plus2.model.pl:

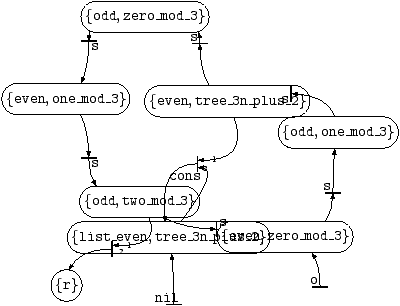
Graphically, this is the alternating tree automaton of Figure 8, again obtained using pl2gastex.

Figure 8: Trees with leaves equal to nil or to 3n+2, or which are lists of even natural numbers

This can be determinized again. Run pldet and auto2pl :

pldet list_even_union_tree3plus2.model.pl \
  | auto2pl - >list_even_union_tree3plus2_d.pl

and you get

As you may see, the determinized automaton is much larger this time, and pl2gastex now has real trouble trying to draw it. (See Figure 9.) We use twopi as graph layout engine here instead of neato and run:

pl2gastex -v -layout twopi \
  -overlap false \
  list_even_union_tree3plus2_d.pl \
   >list_even_union_tree3plus2_model_d.tex

Figure 9: Determinizing the automaton of Figure 8

The trick we have used to compute intersections and unions, namely concatenating files and adding new clauses (provided the concatenated files agree on the semantics of predicates), can also be used to compute other combinations of tree languages. A particularly interesting one is the computation of transitive closures of relations defined by tree automata (or, more generally, by H₁ clause sets).

For the purpose of illustration, imagine you want to compute the transitive closure of the binary relation r defined in rinter_d.pl (drawn in Figure 7, Section 3.3.6). Just create a fresh binary predicate symbol r⁺, and add the clauses

`r`⁺ (X, Y)	:-	`r` (X, Y)
`r`⁺ (X, Z)	:-	`r` (X, Y), `r` (Y, Z)

Concretely, run

OUT=rinter_d_plus
pl2tptp rinter_d.pl >$OUT.p
echo "input_clause (r_plus_r, axiom, \
        [++r_plus(X,Y), --r(X,Y)])." >>$OUT.p
echo "input_clause (r_plus_tc, axiom, \
        [++r_plus(X,Z), --r_plus(X,Y), --r_plus(Y,Z)])" >>$OUT.p

Compute an equivalent non-deterministic tree automata by

h1 -no-trim -no-alternation rinter_d_plus.p

You get

Since the clauses defining r⁺, i.e., r_plus, are the same as those defining r, the transitive closure of r is r⁺ itself here: r was already transitive. (Exercise: why?)

3.3.8 Complete Deterministic Tree Automata, Taking Complements

We observed in Section 3.3.6 that a deterministic tree automaton could be seen as a partial function I_f from tuples of predicates to predicates, one for each function symbol f.

A complete deterministic tree automaton is a set of Horn clauses of the form (5), i.e.,

P (f (X₁, …, X_n))

P₁ (X₁), …, P_n (X_n)

where X₁, ..., X_n are pairwise distinct variables, and where there is exactly one such clause for each (n+1)-tuple (f, P₁, …, P_n) (instad of at most one such clause for incomplete automata).

Any deterministic tree automaton can be completed to a complete one, by adding a catch-all state __all (shown as ⊤ by pl2gastex), to which all missing transitions are directed. Precisely, if there is an (n+1)-tuple (f, P₁, …, P_n) such that there is not clause as above, then add the clause

__all (f (X₁, …, X_n)) :- P₁ (X₁), …, P_n (X_n)

This must also be done whenever any one of P₁, ..., P_n is the catch-all state __all.

The function I_f is then total. The collection of all such I_f defines a finite model, whose set of values is that of all predicates. A value satisfies a predicate P if and only if it is P, seen as a value.

In fact, finite models and complete deterministic tree automata are exactly the same notion. You might want to ponder this.

As an example, let us return to the Dreadsbury mansion murder mystery (Section 3.2). As we have seen, the only to have possibly killed Aunt Agatha is Aunt Agatha herself. We have proved this by showing that the set of clauses in butler-puzzle.p (and explained in Section 3.2) with WHO defined as agatha was satisfiable.

Since this set is satisfiable, it has a model. Well, h1 computes such a model, in the guise of an alternating tree automaton. Run

cpp -P -DWHO=agatha butler-puzzle.p >agatha.p
h1 -no-trim agatha.p

and you'll get it in file agatha.model.pl (see Figure 10):

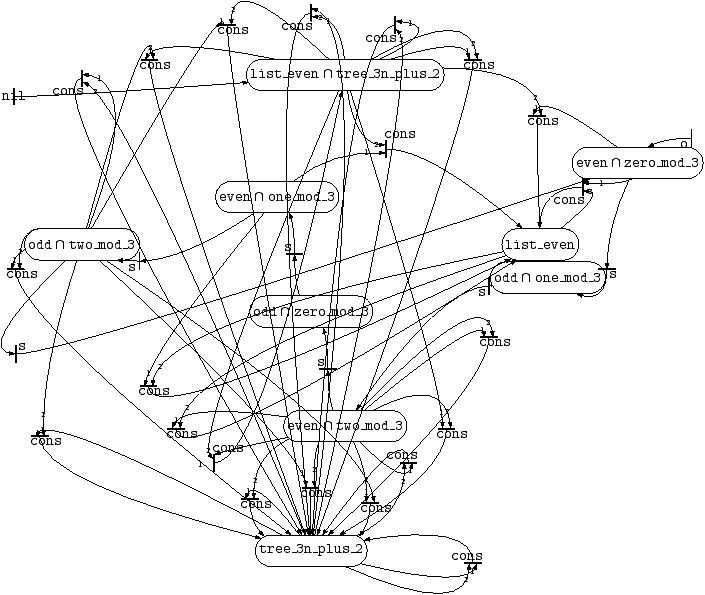
Figure 10: Why Agatha killed herself

All right, this does not look like a model at all (much less an explanation!), but remember there is a complete deterministic tree automaton that is equivalent to it. We know how to compute an equivalent deterministic tree automaton, using pldet and auto2pl, viz.

pldet agatha.model.pl | auto2pl - >agatha_d.pl
pl2gastex -v agatha_d.pl >agathad.tex

Using pl2gastex, as usual, produces a visual representation of it, see Figure 11;

Figure 11: Why Agatha killed herself, deterministically

So Agatha killed herself, Agatha is the only one not to be richer than Agatha, Agatha hates herself and Charles, the butler hates Agatha and Charles, and Charles hates noone.

Let us now produce the corresponding complete deterministic tree automaton. This can be done using auto2pl, which we have already seen, using the -complete 1 option. Be warned, though, that complete deterministic tree automata are large: with n states (included the catch-all states), any function taking k arguments will contribute n^k clauses, never less—and do not forget that any k-ary predicate symbol P with k≥ 2 creates an invisible function symbol f_P, which will contribute n^k clauses as well. Anyway, run

pldet agatha.model.pl | auto2pl -complete 1 - | sort >agatha_c.pl

and you'll get the resulting complete deterministic tree automaton in file agatha_c.pl.

3.4 The Needham-Schroeder Symmetric Key Protocol Example

Try another example, nspriv.p, an encoding of the Needham-Schroeder symmetric key protocol, together with three queries. We do not mean that this is the only possible description of this protocol, and only use this example as a motivation for using h1 with more complex clause sets.

Here are the clauses of nspriv.p, in Prolog notation. We have shown the name of the clause on the left. First, we define a predicate knows that is meant to recognize all messages that a malevolent intruder is able to build. The first clauses say that attackers can build any list of messages provided it knows each message in the list, and conversely that it can build any message that appears at any position in a list it knows:

`intruder_knows_nil`	`knows` (nil)
`intruder_can_take_first_components`	`knows` (M₁)	:-	`knows` (cons (M₁, M₂))
`intruder_can_take_second_components`	`knows` (M₂)	:-	`knows` (cons (M₁, M₂))
`intruder_can_build_pairs`	`knows` (cons (M₁, M₂))	:-	`knows` (M₁), `knows` (M₂)

Lists such as [M₁, M₂, …, M_n] are encoded, very classically, as terms cons (M₁, cons (M₂, … cons (M_n, nil) …)), whence the clauses above. Using a binary symbol crypt to denote encryption, i.e., crypt (M, K) denotes the result of encrypting M using key K, we may also write the following two important rules, stating that the intruder can always encrypt any message it knows using any message it knows, used as a key; and conversely, that the intruder can always decrypt a message if he has the right key.

`intruder_can_encrypt`	`knows` (crypt (M, K))	:-	`knows` (M), `knows` (K)
`intruder_can_decrypt_if_has_private_key`
	`knows` (M)	:-	`knows` (crypt (M, key (pub, K))),
			`knows` (key (prv, K))
`intruder_can_decrypt_if_has_public_key`
	`knows` (M)	:-	`knows` (crypt (M, key (prv, K))),
			`knows` (key (pub, K))
`intruder_can_decrypt_if_has_symmetric_key`
	`knows` (M)	:-	`knows` (crypt (M, key (sym, X))),
			`knows` (key (sym, X))

The last three clauses state how the intruder may decrypt a message of the form crypt (M, Z). We assume that keys come into three varieties, public keys of the form key (pub, K) where K is typically the name of the agent holding this public key; private keys of the form key (prv, K) where K is the name of the agent holding this private key; and symmetric keys of the form key (sym, X), where X is arbitrary. The last three clauses state that you may decrypt a message encrypted with a public key key (pub, K) provided you know the corresponding private key key (prv, X); that you may decrypt a message encrypted with a private key provided you know the corresponding public key; and that you may decrypt a message encrypted with a symmetric key provided you know the latter.

We also assume that there is an operation s that builds a new message s (M) from an old M, in bijection with M; while we can compute s (M) from M and recover M from s (M), the point is that M and s (M) always differ.

`intruder_can_compute_successors`	`knows` (s (M))	:-	`knows` (M)
`intruder_can_compute_predecessors`	`knows` (M)	:-	`knows` (s (M))

In the Needham-Schroeder symmetric key protocol, Alice and Bob communicate with a trusted server to get a common private key that only they know, not the intruder. Alice can always start a session of the protocol and send the server a triple containing Alice's identity alice, Bob's identity bob, and a nonce, that is, a fresh message for this session. Following [2001 (Blanchet)], we encode this nonce as a function symbol applied to all parameters currently known, say noncea (alice, bob)—the function symbol noncea applied to Alice's identity alice and Bob's identity bob. Now we assume a worst-case intruder model, where any communication can be diverted by the intruder. The net effect is that, from a security viewpoint, what Alice does by sending a message consists exactly in making it known to the intruder:

`alice_sends_message_1_to_server`	`knows` (	cons (	alice,
		cons (	bob,
		cons (	noncea (alice, bob),
			nil))))

If the server ever receives such a message, i.e., a message of the form cons (A, cons (B, cons (Na, nil))) for some arbitrary messages A, B, and Na (the server has no way of checking that Alice indeed sent the right message, and can only check the message it receives contains three fields), then it should send out (to Alice, but we have already seen this was irrelevant from a security point of view) the message crypt ([Na, B, K_ab, crypt ([K_ab, A], K_bs)], K_as), where K_ab is some fresh key to be used by Alice and Bob, K_as is a long-term key shared between Alice and the server, and K_bs is a long-term key shared between Bob and the server.

Just like sending a message consists exactly in making it known to the intruder, receiving a message is modeled by stating that the intruder was able to build this message. We shall therefore write a clause saying that, if knows [A, B, Na] then knows crypt ([Na, B, K_ab, crypt ([K_ab, A], K_bs)], K_as). Note that we are effectively saying that, from the angle of security, the actions of the server amount to adding new capabilities to the intruder: if the intruder knows a message matching what the server expects, it can build the message that the server will answer, even though it may not know the long-term keys K_as and K_bs.

Now we encode K_as as the term key (sym, cons (A, cons (server, nil))), and K_bs as the term key (sym, cons (B, cons (server, nil))); note that A and B are variables here, representing the fact that the server will find these keys by looking up tables by the identities of A, resp. B. In current sessions, we encode K_ab by the term key (sym, current_session (A, B, Na)). The key K_ab as generated during older sessions is encoded by the term key (sym, old_session (A, B, Na)). Separating current from old sessions means we have to write two clauses:

`server_answers_A_with_encrypted_packet`
	`knows` (crypt (	cons (	Na,
		cons (	B,
		cons (	key (sym, current_session (A, B, Na)),
		cons (	crypt (cons (key (sym, current_session (A, B, Na)),
			cons (A, nil)),
			key (sym, cons (B, cons (server, nil)))),
			nil)))),
		key (	sym, cons (A, cons (server, nil)))))
			:- `knows` (cons (A, cons (B, cons (Na, nil))))
`intruder_knows_previous_server_messages`
	`knows` (crypt (	cons (	Na,
		cons (	B,
		cons (	key (sym, old_session (A, B, Na)),
		cons (	crypt (cons (key (sym, old_session (A, B, Na)),
			cons (A, nil)),
			key (sym, cons (B, cons (server, nil)))),
			nil)))),
		key (	sym, cons (A, cons (server, nil)))))
			:- `knows` (cons (A, cons (B, cons (Na, nil))))

All right, now, when Alice receives the message from the server, she should send the part encrypted with K_bs to Bob. The idea is that while Alice can decrypt the whole message, which is encrypted with K_as, only Bob can decrypt the sub-message that is encrypted with K_bs. The message that Alice receives from the server should be crypt ([Na, B, K_ab, crypt ([K_ab, A], K_bs)], K_as), however she can only check that it is of the form crypt ([Na, B, K_ab, Msg) for some sub-messages K_ab and Msg (which may be totally unrelated to what the server actually sent). She can however check that Na is the nonce noncea (alice, bob) that she created earlier (see above, clause alice_sends_message_1_to_server), and that B really is Bob's identity bob. So Alice expects a message of the form crypt ([noncea (alice, bob), bob, K_ab, Msg], K_as). As we have said before, for Alice to receive this message, the intruder must send it to Alice, so the intruder must be able to build it. Once Alice receives this, it extract the sub-message Msg and forwards it to Bob—in fact adding it to the set of messages known to the intruder:

`alice_gets_server_message_and_forwards_submessage_to_bob`
	`knows` (Msg)	:- `knows` (crypt (	cons (noncea (alice, bob),
			cons (bob,
			cons (Kab,
			cons (Msg, nil)))),
			key (sym, cons (alice, cons (server, nil)))))

We use an auxiliary predicate alice_key meant to recognize all possible values of Kab above. This is the key as seen by Alice.

`alice_gets_server_message_and_stores_current_session_key`
	`alice_key` (Kab)
		:- `knows` (crypt (	cons (noncea (alice, bob),
			cons (bob,
			cons (Kab,
			cons (Msg, nil)))),
			key (sym, cons (alice, cons (server, nil)))))

Let's see what Bob does in this protocol. First, Bob expects to receive the sub-message Msg above. Cutting it short, Bob decrypts it, gets K_ab, then sends a confirmation challenge crypt (N_b, K_ab), where N_b is a fresh nonce. As before, N_b is modeled as a function symbol nonceb applied to all relevant variables.

`agent_B_gets_forwarded_submessage_and_sends_confirmation_challenge`
	`knows` (crypt (nonceb (Kab, A, B), Kab)	:-	`knows` (crypt (cons (Kab, cons (A, nil)),
			key (sym, cons (B, server, nil))))))

On receiving this challenge, Alice tries to decrypt it with its own version of the key K_ab, and sends back N_b+1:

`alice_answers_confirmation_challenge`
	`knows` (crypt (s (Nb), Kab))	:-	`alice_key` (Kab), `knows` (crypt (Nb, Kab))

Bob then checks that it indeed gets the confirmation message above with the right value for Nb. If so, we store the key Kab in the predicate bob_key:

`agent_B_checks_confirmation_from_A`
	`bob_key` (Kab)	:-	`knows` (crypt (s (nonceb (Kab, A, B)), Kab))

This terminates the description of the protocol. Let us now describe additional things the intruder know. First, the intruder is assumed to know the identities of all agents. We also list who we think are agents. Note that the intruder itself is considered an agent, and has its own identity intruder.

`alice_is_an_agent`	`agent` (alice)
`bob_is_an_agent`	`agent` (bob)
`server_is_an_agent`	`agent` (server)
`intruder_is_an_agent`	`agent` (intruder)
`intruder_knows_all_agents`	`knows` (X)	:-	`agent` (X)

We also posit that the intruder knows all public keys (... because this is what we mean for them to be public!), and its own private key. We also assume that older sessions are so old that the intruder eventually managed to crack all old sessions key. This is slightly pessimistic. But it is precisely the purpose of changing session keys to prevent intruders from gaining anything from cracking old session keys.

`intruder_knows_every_public_key`	`knows` (key (pub, X))
`intruder_knows_own_private_key`	`knows` (key (prv, intruder))
`intruder_knows_all_previous_session_keys`	`knows` (key (sym, old_session (A, B, Na)))

This is all, at last.

Let us now ask a few queries. The first asks whether the intruder may know the key K_ab as it was generated by the server. The second asks whether the intruder may know any key that Alice accepted as being a key K_ab at the end of the protocol. The third asks whether the intruder may know any key that Bob accepted as being K_ab at the end of the protocol.

`intruder_knows_session_key_generated_by_server`
	`false`	:-	`knows` (key (sym, current_session (alice, bob, Na)))
`intruder_knows_session_key_as_seen_by_alice`
	`false`	:-	`alice_key` (key (Mode, current_session (X, Y, N))),
			`knows` (key (Mode, current_session (X, Y, N)))
`intruder_knows_session_key_as_seen_by_B`
	`false`	:-	`knows` (crypt (s (nonceb (Kab, A, B)), Kab)), `knows` (Kab)

Now launch h1 on nspriv.p:

h1 nspriv.p

You should get

*** Derived: intruder_knows_session_key_as_seen_by_B ***

This means in short that h1 believes that this clause set is unsatisfiable; in terms of protocols, that there is an attack. You cannot actually be sure that this is indeed an attack, i.e., that this clause set is indeed unsatisfiable, because this clause set is not in the H₁ format. (You should not conclude from this that cryptographic protocols always produce clause sets outside H₁, see [2002 (Nielson et al.)].)

In this case, and contrarily to the example of Section 3.2, h1 computes an approximation of the input clause set S as a clause set S₁, and reasons on S₁ instead. Check it using the -check-h1 2 option:

h1 -check-h1 2 nspriv.p

and you'll get the list of all clauses in nspriv.p that are not in H₁:

Warning: clause server_answers_A_with_encrypted_packet has non-linear head, variable A occurs repeatedly. Warning: clause intruder_knows_previous_server_messages has non-linear head, variable A occurs repeatedly. Warning: clause agent_B_gets_forwarded_submessage_and_\ \sends_confirmation_challenge has non-linear head, variable Kab occurs repeatedly. Warning: clause alice_answers_confirmation_challenge has two non-sibling variables in the head that are connected in the body, Nb and Kab. Stop.

Note also that h1 gives you an explanation of what's going wrong. For further explanation of what linear terms, sibling variables and connected variables are, see [2002 (Nielson et al.)] or [2005 (Goubault-Larrecq)].

The -check-h1 1 option runs the same checks. However, it still proceeds with checking the (un)satisfiability of the approximated clause set S₁, even when the approximation is not exact, i.e., when the original clause set S is not in H₁.

The approximated clause set S₁ is always in the class H₁, and always implies S logically. In particular, if h1 does not find any contradiction, i.e., if S₁ is satisfiable, then S is satisfiable, too. In terms of cryptographic protocols, if h1 tells you that your protocol has no attack, then you can be sure of it. (That is, up to the accuracy of your model, written as clauses.)

In our case, h1 found a purported attack, i.e., a purported contradiction. It turns out that nspriv.p is indeed contradictory. In fact, in most cases where h1 thinks a clause set is contradictory, it is indeed contradictory. (Although, as usual, your mileage may vary.)

We terminate this example by mentioning the -all option.

The answer

*** Derived: intruder_knows_session_key_as_seen_by_B ***

above means that h1 found a (purported) contradiction first, and second that, in order to derive the empty clause false, h1 required the clause intruder_knows_session_key_as_seen_by_B. Is this the only query that fails? Remember we have asked three queries. One way of checking this is to remove the intruder_knows_session_key_as_seen_by_B clause from nspriv.p and run h1 again. There is a simpler option: run h1 with the -all option. Once a contradiction has been found, instead of stopping just like any other prover, h1 -all will continue, trying to find contradictions using other queries.

On the example, running

h1 -all nspriv.p

you will get the same answer as above:

*** Derived: intruder_knows_session_key_as_seen_by_B ***

In other words, no other query fails. In terms of security, this means that while Bob's key K_ab is not secure, those of Alice and the server definitely are. This may seem paradoxical, however the attack that h1 just found is one where the intruder deceives Bob into accepted an old, cracked key from an older session. This key is not the key that the server produced. It is also old, meaning that it will be detected as not being new by Alice's use of the nonce N_a.

We have just proved that Alice and the server were in fact safe in this protocol, while Bob is not.

The -no-resolve option can be used to disable the reasoning facilities of h1 altogether. Then h1 -no-resolve will just compute an approximation of the input clause set, and store it into the log file. For example,

h1 -no-resolve nspriv.p

runs without any output, and creates the log file nspriv.log.gz. As we have already said, it is not really instructive to look at this file directly. However, you can extract from it the approximated clause set by running:

h1getlog processed nspriv.log | pl2tptp -

This will output the approximated clause set on stdout: h1getlog with the processed option will extract the approximate clauses and print them in Prolog format. Then pl2tptp with the - argument (meaning stdin) will convert these from Prolog format to TPTP format.

All this can be done in a simpler way, by using the -log-out option to h1. Then h1 will output its log file to stdout. You can then pipe it to h1getlog and pl2tptp, as follows.

h1 -log-out -no-resolve nspriv.p | h1getlog processed | pl2tptp -