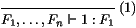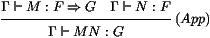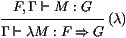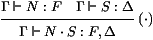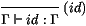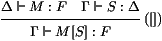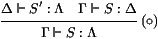Calculs à substitutions explicites

2 Calculs à substitutions explicites

Les combinateurs de Curry ayant trop de défauts en pratique, on peut s'orienter vers d'autres formalismes permettant de coder les λ-termes sous forme de termes du premier ordre, sans liaison de variables.

2.1 Termes de de Bruijn

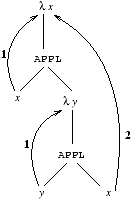
Une solution est d'utiliser des indices de de Bruijn. L'idée est de remplacer toute variable liée x par un pointeur vers l'abstraction qui la lie. On peut représenter ceci logiquement en représentant ce pointeur par un entier, qui compte le nombre de symboles λ que l'on rencontre lorsqu'on remonte l'arbre de syntaxe abstraite depuis l'occurrence considérée de x vers le λ qui la lie. Dans le terme λ x ⋅ x (λ y ⋅ yx) par exemple, dont l'arbre de syntaxe abstraite est:

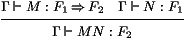la première occurrence de x est liée par la première λ en remontant (son numéro de de Bruijn est 1), l'occurrence de y est liée par la première λ en remontant (son numéro de de Bruijn est aussi 1), et la deuxième occurrence de x est liée par la deuxième λ en remontant, son numéro de de Bruijn est donc 2.

Les noms des variables liées ne servent alors plus à rien, on peut donc les effacer. On peut laisser les variables libres telles quelles, la syntaxe des λ-termes en notation de de Bruijn sera donc:

Λ_db =_def V | N | λ Λ_db | Λ_db Λ_db

La traduction des λ-termes usuels vers ceux en notation de de Bruijn se fait à l'aide de la fonction u ↦ u^db (l), où l est une liste l(1), ..., l(n) de noms de variables:

x^db (l)	=_def	i	si i est le plus petit entier tel que x=l(i)
		x	si x n'apparaît pas dans l
(uv)^db (l)	=_def	u^db (l) v^db (l)
(λ x ⋅ u)^db (l)	=_def	λ (u^db (x::l))

La traduction u^db est définie comme u^db (є), où є est la liste vide.

Une autre façon de calculer u^db est comme en section 1: on définit une fonction d'abstraction M ↦ [x] M, qui fabrique λ appliqué à M dans lequel tous les x ont été remplacés par un plus le nombre de λ au-dessus d'eux dans M. Formellement:

[x] M =_def λ (Abs_x¹ (M))

Abs_xⁿ (x)	=_def	n
Abs_xⁿ (y)	=_def	y (y≠ x)
Abs_xⁿ (m)	=_def	m
Abs_xⁿ (MN)	=_def	Abs_xⁿ (M) Abs_xⁿ (N)
Abs_xⁿ (λ M)	=_def	λ (Abs_xⁿ⁺¹ (M))

On peut alors définir:

x^db	=_def	x
(uv)^db	=_def	u^db v^db
(λ x ⋅ u)^db	=_def	[x] u^db

Calculer u [x:=v] dans cette traduction (lorsque x n'est ni lié ni libre dans u, et aucune variable libre de v n'est liée dans u) est très facile: (u [x:=v])^db = u^db [x:=v^db].

La difficulté dans cette notation est de calculer le réduit de (λ x ⋅ u) v, c'est-à-dire de remplacer l'indice 1 (si on ignore les λ) dans u par v. En-dessous des λ, ce n'est plus l'indice 1 mais un indice 2 ou plus qu'il faudra remplacer. On définit donc une fonction de substitution u [n ← v] où n est un indice ≥ 1, comme suit: (u₁ u₂) [n ← v] =_def u₁ [n ← v] u₂ [n ← v], (λ u) [n ← v] =_def λ (u [n+1 ← v]), mais le calcul est plus compliqué sur les indices eux-mêmes. Si m<n, m [n ← v] représente le remplacement de x qui est liée n lambdas plus haut dans une variable y liée plus bas: le nombre de lambdas à remonter pour retrouver y après la substitution reste le même, donc m [n ← v] =_def m. Si m>n, au contraire, il fallait remonter plus haut que la λ de x pour retrouver la λ liant y; mais la λ de x disparaît au cours de la β-réduction, donc après substitution il n'y a plus que m−1 lambdas à traverser: m [n ← v] =_def m−1 si m>n. Finalement, si m=n, intuitivement n [n ← v] devrait valoir v.

En fait, c'est encore une fois plus compliqué, parce que tous les indices de de Bruijn correspondant à des variables libres dans v mais liée plus haut doivent voir leurs indices changer. Par exemple, considérons λ y ⋅ (λ x,z ⋅ x) y, qui s'écrit λ ((λ λ 2) 1) en notation de de Bruijn et se réduit en λ ((λ 2) [1 ← 1]) = λ (λ (2 [2 ← 1])). Ce dernier terme doit être la notation de de Bruijn de λ y, z ⋅ y, c'est-à-dire λ λ 2. Autrement dit, 2 [2 ← 1] =_def 2. En effet, 1 représente la variable y, qui est liée par le premier λ. Mais comme on l'installe à l'occurrence de x qui est sous un λ z supplémentaire, il faut incrémenter 1 pour lui faire traverser le λ z. Formellement, m [n ← v] doit donner v dans lequel (en ignorant les λ pour l'instant) les indices de v qui sont ≥ 1 doivent être incrémentés de n−1 (les n lambdas de λ x ⋅ u au-dessus de l'occurrence considérée de x, moins un à cause du λ x qui disparaît). Donc n [n ← v] =_def U₀ⁿ (v), où U_kⁿ est la fonction de mise à jour qui incrémente de n−1 les indices de v qui sont >k. La raison d'être de l'indice k est, encore une fois, due au fait que nous aurons à traverser des λ. On définit donc finalement:

U_kⁿ (MN)

=_def

U_kⁿ (M) U_kⁿ (N)

U_kⁿ (λ M)

=_def

λ (U_k+1ⁿ (M))

U_kⁿ (x)

=_def

U_kⁿ (p)

=_def

⎧
⎨
⎩

p+n−1	si p>k
p	sinon

puis la substitution:

(MN) [n ← P]

=_def

M [n← P] N [n ← P]

(λ M) [n ← P]

=_def

λ (M [n+1 ← P])

x [n ← P]

=_def

m [n ← P]

=_def

⎧
⎨
⎩

m	si m<n
U₀ⁿ (P)	si m=n
m−1	si m>n

La β-réduction en notation de de Bruijn est alors la plus petite relation passant au contexte telle que:

(λ M) N → M [1 ← N]

Il se trouve que si u → v par β-réduction, alors u^db → v^db par la règle ci-dessus, mais la vérification est assez longue, et nous allons nous intéresser à un formalisme proche mais plus élémentaire, le λσ-calcul. (Nous considérerons une variante de celui de [ACCL90], qui ne lui est pas identique.)

2.2 Le λσ-calcul

L'intérêt du λσ-calcul est qu'il remplace la notion complexe de substitution M [n ← N] d'indices de de Bruijn par une série de règles de réécriture sur des termes du premier ordre, comme pour les combinateurs S, K et I. Mais contrairement aux combinateurs, le λσ va interpréter correctement la β-réduction, ce qui va nous permettre de réaliser de véritables machines à réduction pour le λ-calcul.

Bien que le λσ-calcul soit très proche du calcul avec indices de de Bruijn, il est utile de le décrire en partant de considérations plus élémentaires. En particulier, nous allons le motiver à partir de considérations de codage et de typage.

En λσ, on garde les opérateurs d'application (binaire, invisible) et d'abstraction λ, ainsi que l'indice 1. Intuitivement, la règle de typage simple de 1 est:

Autrement dit, supposons que l'on ait empilé la valeur de la variable 1 (de type F₁) au-dessus de la valeur de 2 (de type F₂), ..., au-dessus de la valeur de n (de type F_n). Alors 1 récupére la valeur au sommet de la pile, de type F₁. La règle de typage de l'application va de soi:

où Γ est une liste de types (on dira aussi que Γ est un type de piles). La règle de typage de l'abstraction est, de même, la règle d'introduction de l'implication:

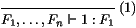
Noter que F, Γ est une liste, obtenue en ajoutant F en tête de la liste Γ. Contrairement aux systèmes de typage de la partie 2, les formules ne peuvent pas être permutées dans un type de pile. Cette règle signifie que λ M est une fonction qui, dans une pile de type Γ, va d'abord empiler un argument (la valeur de 1, de type F), sur la pile, puis évaluer le corps M, de type G. On obtient ainsi une fonction de F vers G.

Pour réduire (λ M) N, il faut donc placer la valeur de N sur la pile, puis évaluer M dans la nouvelle pile. Notons ⋅ l'opérateur infixe qui prend un terme N et une pile S, et retourne N ⋅ S, à savoir la pile S avec N empilé par-dessus. On a la règle de typage:

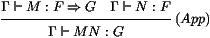
Dans une pile courante S₀ de type Γ, pour obtenir la pile N ⋅ S₀ obtenue en empilant N au-dessus de S₀, nous devons d'abord recopier S₀. Ceci s'effectue par l'usage de la pile id, qui retourne la pile courante:

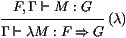
On obtient ainsi une pile N ⋅ id de type F, Γ, qui est obtenue en ajoutant N au sommet de la pile courante. Il ne reste plus qu'à évaluer M dans cette pile. Pour ceci, on introduit un opérateur binaire _ [_]: M [S] évalue M dans la pile S. On a la règle de typage:

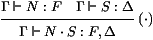
Ceci mène à la règle de β-réduction:

(λ M) N → M [N ⋅ id]

Noter qu'on a juste une constante 1 représentant la variable 1, mais aucune autre variable 2, 3, ..., au moins pour l'instant. Nous les coderons un peu plus loin. Il ne reste alors plus qu'à propager les substitutions S dans les termes M [S]. Regardons pour ceci la forme de M. Les substitutions commutent avec les applications, donc (M₁ M₂) [S] → M₁[S] M₂[S]. Si M = 1, alors on voit que 1 [S] va récupérer le premier élément de la pile S, donc 1 [N ⋅ S] → N, et 1 [id] → 1 (en fait, demander M [id] → M semble raisonnable, que ce soit opérationnellement, ou par raisonnement sur les types). Si M est de la forme M' [S'], il est tentant de réécrire M' [S'] [S] en M' [S' ∘ S], où ∘ est un opérateur de composition de substitutions, typé par:

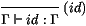
L'usage d'un tel opérateur n'est pas en fait indispensable, et il existe des calculs à substitutions explicites qui ne l'ont pas, comme le λυ-calcul [LRD94].

La seule difficulté est de définir M [S] lorsque M est une abstraction, autrement dit M = λ M'. Intuitivement, M [S] doit se réduire en une abstraction λ (M' [S']), où S' est une pile à trouver. Ici le typage va nous aider. Supposons Γ ⊢ S : Δ, et F, Δ ⊢ M' : G, de sorte que Γ ⊢ M [S] : F ⇒ G. Alors on veut que Γ ⊢ λ (M' [S']) : F ⇒ G, donc on doit avoir F, Γ ⊢ S' : F, Δ. Opérationnellement, on veut que S' enlève l'élément 1 de la pile courante (l'argument de la λ, de type F), calcule la pile S (qui n'est valide qu'en-dehors de la λ), puis réempile l'argument de type F. On y arrivera par exemple en ajoutant un opérateur de dépilement ↑ (shift):

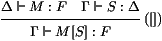
qui retourne la pile obtenue après en avoir supprimé l'élément au sommet. On peut alors poser:

(λ M') [S] → λ (M' [1 ⋅ (S ∘ ↑)])

Maintenant que nous avons ↑ et ∘, on peut au passage représenter toutes les variables de de Bruijn. Il suffit de poser:

=_def

1 [↑ⁿ⁻¹]

pour tout n≥ 2, où ↑¹ =_def ↑ et ↑ⁿ⁺¹ =_def ↑ ∘ ↑ⁿ pour tout n≥ 1. En particulier, 2 =_def 1 [↑], 3 =_def 1 [↑ ∘ ↑], etc.

Nous avons ajouté de nombreux opérateurs, et il faut en théorie de nouveau définir comment les substitutions se propagent à travers ces nouveaux opérateurs. Ceci se fait assez intuitivement, et nous présentons donc la définition formelle du λσ-calcul (non typé).

Bien que ce calcul soit non typé, il est intéressant de garder une forme faible de typage, avec deux types, celui des termes et celui des substitutions explicites, ou piles. Ceci définit deux ensembles T et S des termes et des piles respectivement, définis par la syntaxe:

T	=_def	V_T \| T T \| λ T \| 1 \| T [ S]
S	=_def	V_S \| ↑ \| id \| S ∘ S \| T ⋅ S

Noter que ceci nous force à distinguer deux sortes de variables, les variables de termes (dans V_T) et les variables de piles (dans V_S).

Les règles de réduction sont données en figure 1.

(β) (λ M) N → M [N ⋅ id]

([id]) M [id] → M (η⋅) 1 ⋅ ↑ → id

(∘ id) S ∘ id → S (η⋅∘) (1 [S]) ⋅ (↑ ∘ S) → S

(id∘) id ∘ S → S

([]) (M [S]) [S'] → M [S ∘ S']

(∘) (S ∘ S')∘ S'' → S ∘ (S' ∘ S'')

(1) 1 [N ⋅ S] → N

(↑) ↑ ∘ (N ⋅ S) → S

(⋅) (M ⋅ S) ∘ S' → (M [S']) ⋅ (S ∘ S')

(λ) (λ M) [S] → λ (M [1 ⋅ (S ∘ ↑)])

(app) (M N) [S] → (M [S]) (N [S])

Figure 1: Les règles de réduction de λσ

Toutes les règles sauf (η⋅) et (η⋅∘) sont justifiées par des arguments comme ceux utilisés ci-dessus. Les deux règles (η⋅) et (η⋅∘) sont nécessaires pour être sûr que λσ est localement confluent. En effet, (λ M) [id] peut se réduire soit à λ M par ([id]), soit à λ (M [1 ⋅ (id ∘ ↑)]) par (λ). Ce dernier terme se réduit à λ (M [1 ⋅ ↑]), mais pas à λ M sauf si on ajoute la règle (η⋅). Mais une fois cette dernière règle ajoutée, (1 ⋅ ↑) ∘ S peut se réduire soit à S par (η⋅), soit à (1 [S]) ⋅ (↑ ∘ S): la règle (η⋅∘) est nécessaire pour réduire ce dernier à S.

L'ensemble de toutes les règles sauf (β) est appelé σ, c'est le calcul de propagation des substitutions à travers les termes. Le système de réécriture tout entier est appelé λσ.

2.3 Propriétés de λσ

Étudions les propriétés théoriques de λσ. D'abord, λσ simule bien la β-réduction (théorème 3). La traduction standard des λ-termes en λσ-termes est similaire à celle des λ-termes en termes de de Bruijn:

x^* (l)	=_def	i =_def 1 (si i=1), 1 [↑ⁱ⁻¹] (sinon)	si i est le plus petit entier tel que x=l (i)
		x (si n=0), x [↑ⁿ] (sinon)	si x n'est pas dans l, n est la longueur de l
(uv)^* (l)	=_def	u^* (l) v^* (l)
(λ x⋅ u)^* (l)	=_def	λ (u^* (x::l))

Ceci est similaire à la traduction x^db (l) définie en section 2.1. En fait, la seule différence est la traduction des variables libres (le deuxième cas définissant x^* (l)). Par exemple, (λ x ⋅ xy)^db (є) = λ (1 y), mais (λ x⋅ xy)^* (є) = λ (1 (y [↑])). On aurait pu définir x^* (l) comme étant identique à x^db (l), mais le théorème 3 ne fonctionnerait plus sur les termes avec des variables libres. Noter qu'on ne peut pas définir x^db (l) comme x^* (l), car y [↑] n'est pas une notation qui existe en λ-calcul avec indices de de Bruijn.

Donc λσ simule bien la β-réduction. Ceci n'est pas totalement immédiat, et nous allons prendre quelques détours.

Lemme 3 Le σ-calcul est localement confluent.

Nous n'en donnerons pas de preuve, pour deux raisons. D'abord la vérification de ce fait nécessite la connaissance de la notion de paires critiques et de la théorie associée (cf. [DJ90]). Ensuite, le nombre de paires critiques est assez élevé, et en fait la vérification de confluence locale est un processus totalement automatisable, qui est mieux effectué par une machine que par un être humain.

Ensuite, on constate que la propagation des substitutions est un processus qui termine. Ceci a l'air d'aller de soi, mais c'est loin d'être évident. En fait, le théorème 2 n'a longtemps eu que des preuves beaucoup plus complexes. Nous avons quand même besoin de quelques outils supplémentaires. D'abord, le résultat suivant, d'utilisation générale (notons que λσ est un système de réécriture sur des termes du premier ordre):

Définition 1 Soit F une signature du premier ordre, c'est-à-dire un ensemble dit de symboles de fonction, chaque symbole de fonction f étant associé à un entier appelé son arité α (f). Les termes sur F à variable dans X sont définis inductivement par: toute variable x est un terme, et si t₁, ..., t_n sont des termes et α (f) = n, alors f (t₁, …, t_n) est un terme.

On dit qu'une relation binaire R sur les termes est bonne si et seulement si elle n'admet aucune chaîne infinie décroissante t₁ R t₂ R … R t_k R.

Soit > une relation binaire sur F. On définit l'ordre lexicographique sur les chemins ou lpo (“lexicographic path ordering”) >_lpo comme suit. Pour tous termes s et t, s >_lpo t si et seulement si s est de la forme f (s₁, …, s_m) et:

(i) s_i >_lpo t pour au moins un i, 1≤ i≤ m, ou:
(ii) t est de la forme g (t₁, …, t_n), f > g et s >_lpo t_j pour tout j, 1≤ j≤ n, ou:
(iii) t est de la forme g (t₁, …, t_n), f=g (donc m=n) et s₁ >_lpo t₁, ..., s_k−1 >_lpo t_k−1, s_k >_lpo t_k, s >_lpo t_k+1, ..., s >_lpo t_n pour un certain k, 1≤ k≤ n.

où >_lpo est la clôture réflexive de >_lpo.

La définition du lpo est correcte: c'est une définition par récurrence sur (s, t) ordonné par le produit lexicographique des ordres de sous-termes. Noter le cas subtil du point (iii): après l'indice k, on compare s (le terme de gauche tout entier) à chaque t_j restant.

On peut montrer que si t est un sous-terme strict de s, alors s >_lpo t; que si > est un ordre strict (une relation irréflexive et transitive) alors >_lpo est aussi un ordre strict; que >_lpo est stable par substitutions: si s >_lpo t alors s [x₁:=u₁, …, x_p:=u_p] >_lpo t [x₁:=u₁, …, x_p:=u_p]; que >_lpo passe au contexte: si s >_lpo t alors f (s₁, …, s_k−1, s, s_k+1, …, s_n) >_lpo f (s₁, …, s_k−1, t, s_k+1, …, s_n). Un ordre qui a toutes ces propriétés est appelé un ordre de simplification. Le théorème de Dershowitz dit que si F est fini et > est un ordre strict, alors >_lpo est un bon ordre. C'est un théorème non trivial, qui fait appel notamment au théorème de Kruskal: lire [DJ90] pour les détails.

On va montrer directement que >_lpo est bon, ce qui montrera que le résultat est toujours valable même quand F est infini (à condition que > soit bonne) et > n'est pas un ordre strict:

Théorème 1 Si > est une bonne relation sur F alors >_lpo est bonne sur l'ensemble des termes.

Preuve : Notons SN l'ensemble des termes t accessibles dans >_lpo, c'est-à-dire qui sont tels qu'il n'y a pas de chaîne infinie décroissante t >_lpo t₁ >_lpo … >_lpo t_k >_lpo …. Notre but est donc de démontrer que tout terme t est dans SN. On peut le démontrer par récurrence structurelle sur t; que c'est très proche des démonstrations de forte normalisation de la partie 2, à ceci près qu'on n'a pas besoin de généraliser la terminaison en une propriété de réductibilité d'abord. Mais une démonstration à l'aide de contre-exemples minimaux (quoiqu'équivalente, en logique classique) sera plus claire.

Notons d'abord qu'on peut donner une présentation équivalente mais plus simple du lpo. On a s >_lpo t si et seulement si s = f (s₁, …, s_m) et soit:

(i') s_i >_lpo t pour un i, soit:
(ii') t = g (t₁, …, t_n), s >_lpo t_j pour tout j, et s ≫ t.

On définit f (s₁, …, s_m) ≫ g (t₁, …, t_n) si et seulement si f > g, ou bien f=g et (s₁, …, s_m) >_lpo^lex (t₁, …, t_n).

L'extension lexicographique >^lex d'une relation > sur un ensemble A est par définition la relation sur les suites d'éléments de A telle que (a₁, …, a_m) >^lex (a'₁, …, a'_n) si et seulement si m=n et a₁≥ a'₁, ..., a_k−1 ≥ a'_k−1, a_k > a'_k pour un certain k, 1≤ k≤ n.

Si > est bonne, alors >^lex est bonne: c'est par récurrence double, sur m d'abord, sur a₁ ensuite. (Exercice.)

Notons SN l'ensemble des termes dont les arguments sont tous dans SN. Autrement dit, SN est l'ensemble des termes f (s₁, …, s_m) tels que s₁, ..., s_m sont dans SN.

Par définition de SN, ≫ est bon sur SN. Attention, ceci signifie qu'il n'y a pas de chaîne infinie décroissante le long de ≫ dans SN, mais les chaînes infinies décroissantes peuvent a priori exister; elles ne peuvent cependant pas rester indéfiniment dans SN.

Définissons aussi s ▷ t si et seulement si s s'écrit f (s₁, …, s_m) et t = s_i pour un i, 1≤ i≤ m. Sa clôture transitive ▷⁺ est bonne. C'est l'ordre sous-terme.

Montrons que SN ⊆ SN. Par contradiction, supposons s ∈ SN \ SN. Comme ≫ est bon sur SN, on peut supposer s minimal dans SN \ SN, c'est-à-dire que s ≫ t n'est vrai pour aucun t ∈ SN \ SN: comme ≫ est bon sur SN, il l'est aussi sur SN \ SN, et l'on peut au besoin remplacer s par n'importe laquelle de ses formes normales pour ≫ dans SN \ SN. Le fait que s soit minimal dans SN \ SN signifie:

(a) si s ≫ t et t ∉SN, alors t ∉SN.

Écrivons aussi s = f (s₁, …, s_m), et notons que s_i ∈ SN pour tout i, 1≤ i≤ m, puisque s ∈ SN.

Comme s ∉SN, il existe un t tel que s >_lpo t et t ∉SN. On peut maintenant choisir t minimal pour l'ordre sous-terme ▷⁺. En particulier, et en écrivant t = g (t₁, …, t_n):

(b) pour tout j, 1≤ j≤ n, si s >_lpo t_j, alors t_j ∈ SN.

Exploitons maintenant la définition de s >_lpo t et t ∉SN. Dans le cas (i'), rappelons que s_i ∈ SN. Comme s_i >_lpo t, on a nécessairement aussi t ∈ SN, contradiction. Dans le cas (ii'), on a s ≫ t, et t ∉SN, donc par (a) t n'est pas dans SN. Il existe donc un j, 1≤ j≤ n, tel que t_j ∉SN. En relisant (ii'), on voit que l'on a s >_lpo t_j: donc (b) s'applique, et t_j ∈ SN, contradiction.

Nous avons donc montré SN ⊆ SN. On en conclut que tout terme s = f (s₁, …, s_m) est dans SN, par récurrence structurelle sur s. L'hypothèse de récurrence nous dit en effet que s₁, ..., s_m sont dans SN, c'est-à-dire que s ∈ SN. Donc s ∈ SN. ♦

On peut aussi démontrer que si > est un ordre strict total (pour tous f, g, f > g ou g > f ou f=g), alors >_lpo est un ordre strict total sur les termes clos (sans variables libres). Ceci a des applications en démonstration automatique notamment, mais nous ne l'utiliserons pas.

Corollaire 1 Si toutes les règles l → r d'un système de réécriture R sont telles que l >_lpo r et > est bon, alors R termine.

Preuve : Par le théorème 1 et le fait que >_lpo passe au contexte et est stable par substitutions. ♦

Pour démontrer qu'un système de réécriture R termine, il suffit donc de trouver un bon ordre strict sur les symboles de fonction qui fasse décroître les termes le long de toutes les règles de R.

Théorème 2 Le σ-calcul est fortement normalisant.

Preuve : On peut simplifier le problème. Considérons le système de réécriture suivant, obtenu à partir de σ en remplaçant les _ [_] par des ∘ (on identifie termes et piles), le symbole invisible d'application par ⋅, et en éliminant les règles en double:

(∘ id)	M ∘ id → M	(η⋅)	1 ⋅ ↑ → id
(id∘)	id ∘ S → S	(η⋅∘)	(1 ∘ S) ⋅ (↑ ∘ S) → S
(∘)	(S ∘ S')∘ S'' → S ∘ (S' ∘ S'')
(1)	1 ∘ (N ⋅ S) → N
(↑)	↑ ∘ (N ⋅ S) → S
(⋅)	(M ⋅ S) ∘ S' → (M ∘ S') ⋅ (S ∘ S')
(λ)	(λ M) ∘ S → λ (M ∘ (1 ⋅ (S ∘ ↑)))

Il est facile de voir que si on prend un ordre strict > sur les symboles de fonction tel que 1, ⋅, ↑ > id et ∘ > ⋅, alors les termes décroissent dans >_lpo dans toutes les règles, sauf (λ). Le seul problème est la règle (λ).

Pour régler ce problème, estimons, dans les termes de la forme M ∘ N, sous combien de λ les règles ci-dessus peuvent pousser N. Notons l (M) ce nombre:

l (x)	=_def	0	l (1)	=_def	0
l (↑)	=_def	0	l (λ M)	=_def	l (M) + 1
l (M ⋅ N)	=_def	max(l (M), l (N))
l (id)	=_def	0	l (M ∘ N)	=_def	l (M) + l (N)

Notons que, si M → N, alors l (M) ≥ l (N). En effet, c'est vrai lorsque M est lui-même le rédex contracté (on a même égalité, sauf éventuellement pour les règles (1) et (↑)), et ensuite quelle que soit la profondeur du rédex contracté, parce que l (_) est construite à partir de + et max, qui sont des fonctions monotones.

On va maintenant décorer les symboles de fonction dans les termes (c'est le semantic labelling dû à Hans Zantema). On pose:

[x]	=_def	x	[1]	=_def	1
[↑]	=_def	↑	[λ M]	=_def	λ [M]
[M ⋅ N]	=_def	[M] ⋅ [N]
[id]	=_def	id	[M ∘ N]	=_def	[M] ∘_{l (M)+l (N)} [N]

où l'on considère une infinité de symboles ∘_n, n ≥ 0.

On vérifie alors que, pour toute règle l → r du système ci-dessus, on peut réécrire [M] en [N] par les règles suivantes (par convention, m est l (M), n est l (N), p est l (P)):

(λ M) ∘_m+p+1 P	→	λ (M ∘_m+p (1 ⋅ (P ∘_p ↑)))
1 ∘_{max(m, n)} (M ⋅ N)	→	M
↑ ∘_{max(m, n)} (M ⋅ N)	→	N
id ∘_m M	→	M
M ∘_m id	→	M
(M ∘_m+n N) ∘_m+n+p P	→	M ∘_m+n+p (N ∘_n+p P)
(M ⋅ N) ∘_{max(m, n)+p} P	→	(M ∘_m+p P) ⋅ (N ∘_n+p P)
1 ⋅ ↑	→	id
(1 ∘_m M) ⋅ (↑ ∘_m M)	→	M

Comme M → N implique l (M) ≥ l (N), on en déduit par une récurrence immédiate sur la profondeur du rédex contracté dans M que M → N dans le système sans indices implique [M] →⁺ [N] dans le système de réécriture ci-dessus, plus les règles:

(down) M ∘_n N → M ∘_m N

pour tous n > m. Appelons Subst^* ce système, incluant les règles (down). (Par exemple, si M = M₁ ∘ M₂ et N = N₁ ∘ M₂, avec M₁ → N₁, par hypothèse de récurrence [M₁] →⁺ [N₁], donc [M] →⁺ [N₁] ∘_{l (M₁) + l (M₂)} [M₂] →^* [N₁] ∘_{l (N₁) + l (M₂)} [M₂] = [N] par (down), puisque l (M₁) ≥ l (N₁).)

Or il est maintenant facile de voir que Subst^* termine, en utilisant un lpo >^lpo avec > défini par … > ∘_n+1 > ∘_n > … > ∘₁ > ∘₀ > λ, 1, ⋅, ↑ et 1, ⋅, ↑ > id. ♦

Exercice 13 Montrer que le système de réécriture suivant termine, où D_x est un opérateur censé représenter la dérivation par rapport à x ∂/∂ x:

D_x (x)	→	1
D_x (a)	→	0
D_x (M+N)	→	D_x (M) + D_x (N)
D_x (M × N)	→	D_x (M) × N + M × D_x (N)
D_x (M−N)	→	D_x (M) − D_x (N)
D_x (−M)	→	−D_x (M)
D_x (M/N)	→	(D_x (M) × N − M × D_x (N)) / N²
D_x (log(M))	→	D_x (M) / M
D_x (M^N)	→	N × (M^N−1 × D_x (M)) + M^N × (log(M) × D_x (N))

0+N	→	N	M+0	→	M
S(M)+N	→	S (M+N)	M+S(N)	→	S(M+N)
(M+N)+P	→	M+(N+P)	S(M) − S(N)	→	M−N
0 × N	→	0	M × 0	→	0
S (M) × N	→	M × N + N	M × S(N)	→	M+M× N
(M+M') × N	→	M × N + M' × N	M × (N+N')	→	M× N + M× N'
(M × N) × P	→	M × (N × P)

(1 dénotant S (0), et 2 dénotant S (1).)

Corollaire 2 Le σ-calcul est confluent.

Preuve : Par le lemme de Newman et les résultats précédents. ♦

Théorème 3 Si u → v par β-réduction, alors u^* (l) →⁺ v^* (l) en λσ, pour toute liste l de variables.

Preuve : On prouve une série de lemmes auxiliaires. D'abord, définissons quelques abréviations: ↑^p dénote id si p=0, ↑ si p=1, ↑ ∘ ↑^p−1 sinon; ⇑^p S est S si p=0, ⇑ (⇑^p−1 (S)) sinon, où ⇑ (S) =_def 1 ⋅ (S ∘↑). Notons →_σ la relation de réécriture de σ seul, et =_σ la relation d'équivalence associée.

On remarque les points (1) à (5) suivants.

(1) ↑ ∘ ⇑ (S) →_σS ∘ ↑.

(2) pour tous entiers q≥ 0 et i≥ 1, (q+i) [⇑^q (S)] =_σi [S ∘ ↑^q]. En effet, (q+i) [⇑^q (S)] =_σ1 [↑^q+i−1] [⇑^q (S)] →_σ1 [↑^q+i−1 ∘ ⇑^q (S)] =_σ1 [↑^q+i−2 ∘ (⇑^q−1 (S) ∘ ↑)] (par (1)) =_σ… =_σ1 [↑ⁱ⁻¹ ∘ (S ∘ ↑^q)] =_σi [S ∘ ↑^q].

(3) si i≤ q, i [⇑^q (S)] =_σi. En effet, i [⇑^q (S)] =_σ1 [↑ⁱ⁻¹] [⇑^q (S)] =_σ1 [↑ⁱ⁻¹ ∘ ⇑^q (S)] =_σ1 [↑ⁱ⁻² ∘ (⇑^q−1 (S) ∘ ↑)] =_σ… =_σ1 [↑¹ ∘ ⇑^q−i+2 (S) ∘ ↑ⁱ⁻²] =_σ1 [⇑^q−i+1 (S) ∘ ↑ⁱ⁻¹] =_σ1 [⇑^q−i+1 (S)] [↑ⁱ⁻¹] =_σ1 [↑ⁱ⁻¹] =_σi.

(4) Si y₁, ..., y_p sont p variables n'apparaissant pas dans la liste l et non libres dans v, alors v^* (l) [↑^p] =_σv^* (y₁::…::y_p::l). À cause des λ, nous devrons prouver un résultat plus général, à savoir:

v^* (x₁::…::x_q::l) [⇑^q (↑^p)] =_σv^* (x₁::…::x_q::y₁::…::y_p::l)

si les y_i n'apparaissent pas dans l, ne sont pas libres dans v, et les x_i ne sont pas libres dans v.

C'est par récurrence structurelle sur v. Si v est une variable x apparaissant dans l, soit i le plus petit indice tel que l(i) = x; alors v^* (l) (x₁::…::x_q::l) [⇑^q (↑^p)] = (q+i) [⇑^q (↑^p)] =_σi [↑^p ∘ ↑^q] (par (2)) =_σi+p+q = v^* (x₁::…::x_q::y₁::…::y_p::l), puisque x ne peut être égale à aucune x_i ou y_i par hypothèse.

Si v est une autre variable y, v^* (x₁::…::x_q::l) [⇑^q (↑^p)] =_σy [↑^q+n] [⇑^q (↑^p)] =_σy [↑^n+p+q] (par le même raisonnement que ci-dessus) =_σv^* (x₁::…::x_q::y₁::…::y_p::l), puisque x ne peut être égale à aucune x_i ou y_i par hypothèse.

Si v est une application, c'est évident par hypothèse de récurrence et la règle (app). Si v est une abstraction λ x ⋅ w, alors v^* (x₁::…::x_q::l) [⇑^q (↑^p)] = λ (w^* (x::x₁::…::x_q::l)) [⇑^q (↑^p)] →_σλ (w^* (x::x₁::…::x_q::l) [⇑^q+1 (↑^p)]) (par (λ)) =_σλ (w^* (x::x₁::…::x_q::y₁::…::y_p::l)) par hypothèse de récurrence. Techniquement, ceci suppose que l'on peut choisir x non libres dans v, et donc il faut vérifier que la traduction de deux termes α-équivalents est identique. Cette vérification est omise, car assez rebutante et peu instructive.

(5) si x n'apparaît pas dans l, u^* (x::l) [v^* (l) ⋅ id] =_σ(u [x:=v])^* (l). Encore une fois à cause des abstractions, on va prouver que pour toutes variables y₁, ..., y_m n'apparaissant pas dans l et non libres dans v, et pour tout x n'apparaissant pas dans l:

u^* (y₁::…::y_p::x::l) [⇑^p (v^* (l) ⋅ id)] =_σ(u [x:=v])^* (y₁::…::y_p::l)

C'est par récurrence structurelle sur u. Si u est une λ-abstraction λ y ⋅ w, alors le côté gauche est λ (w^* (y::y₁::…::y_p::x::l)) [⇑^p (v^* (l) ⋅ id)] →_σλ (w^* (y::y₁::…::y_p::x::l) [⇑^p+1 (v^* (l) ⋅ id)]) =_σλ ((w [x:=v])^* (y::y₁::…::y_p::l)) = (u [x:=v])^* (y₁::…::y_p::l), en choisissant y n'apparaissant pas dans l et non libre dans v, à α-renommage près.

Si u est une variable, on a quatre cas. Cas 1: u est une variable y différente de x, y₁, ..., y_p et n'apparaissant pas dans l, alors u^* (y₁::…::y_p::x::l) [⇑^p (v^* (l) ⋅ id)] =_σy [↑^p+n+1] [⇑^p (v^* (l) ⋅ id)] (où n est la longueur de l) =_σy [↑ⁿ⁺¹ ∘ ((v^* (l) ⋅ id) ∘ ↑^p)] =_σy [↑ⁿ ∘ (id ∘ ↑^p)] =_σy [↑^n+p] =_σ(u [x:=v])^* (y₁::…::y_p::l). Cas 2: u apparaît dans l, disons à l'indice i. Alors u^* (y₁::…::y_p::x::l) [⇑^p (v^* (l) ⋅ id)] =_σ1 [↑^p+i] [⇑^p (v^* (l) ⋅ id)] =_σ1 [↑ⁱ ∘ ((v^* (l) ⋅ id) ∘ ↑^p)] =_σ1 [↑^p+i−1] = (u [x:=v])^* (y₁::…::y_p::l). Cas 3: u = y_i, alors u^* (y₁::…::y_p::x::l) [⇑^p (v^* (l) ⋅ id)] =_σi [⇑^p (v^* (l) ⋅ id)] =_σi (par (3)) = (u [x:=v])^* (y₁::…::y_p::l). Cas 4: u = x, alors u^* (y₁::…::y_p::x::l) [⇑^p (v^* (l) ⋅ id)] = (p+1) [⇑^p (v^* (l) ⋅ id)] =_σ1 [(v^* (l) ⋅ i) ∘ ↑^p] =_σv^* (l) ∘ ↑^p =_σv^* (y₁::…::y_p::l) par (4).

Le cas de l'application est immédiat.

De (5) et du fait que (u [x:=v])^* (l) est σ-normal, et que σ est terminant et confluent, on déduit que si x n'apparaît pas dans l, u^* (x::l) [v^* (l) ⋅ id] →_σ^* (u [x:=v])^* (l). (On pourrait le vérifier directement, mais c'est beaucoup plus long.) Donc ((λ x ⋅ u) v)^* (l) = (λ (u^* (x::l))) v^* (l) → u^* (x::l) [v^* (l) ⋅ id] (par (β)) →_σ^* (u [x:=v])^* (l).

Il ne reste qu'à démontrer le résultat par récurrence sur la profondeur du rédex contracté dans u. On vient juste de traiter le cas où cette profondeur vaut 0. Le cas où u est une application est immédiat. Si u est une abstraction λ x ⋅ u₁ avec u₁ → v₁, on a u^* (l) = λ (u₁^* (x::l)) →⁺ λ (v₁^* (x::l)) = v^* (l) (par hypothèse de récurrence). ♦

Le λσ-calcul est localement confluent, comme on peut le vérifier, et comme le λ-calcul est confluent, on peut espérer que le λσ-calcul le soit aussi. Mais:

Théorème 4 Le λσ-calcul n'est pas confluent.

Preuve : Cf. [CHL91]. ♦

Par contre:

Théorème 5 Un λσ-terme est semi-clos si et seulement s'il ne contient aucune variable de pile (dans V_S). Le λσ-calcul semi-clos est le λσ-calcul restreint aux termes semi-clos.

Le λσ-calcul semi-clos est confluent.

Preuve : Ce résultat est dû à Ríos [Río93]. Comme il est très technique, on va démontrer un résultat relativement plus facile, mais qui donne une idée des techniques utilisées: on va démontrer que le λσ-calcul clos — c'est-à-dire sans aucune variable libre— est confluent.

La technique est la suivante. Supposons qu'on sache construire un foncteur F, c'est-à-dire une fonction qui traduit des λσ-termes M en des termes F (M) dans un langage L et qui préserve les réécritures: si M →^* N alors F (M) →^* F (N) dans L. Si on sait que L est confluent, alors on peut clore le diagramme suivant avec un terme u de L:

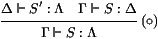
Si en plus on a un foncteur G de L vers λσ tel que N →^* G (F (N)), alors on aura N₁ →^* G (F (N₁)) →^* G (u) et N₂ →^* G (F (N₂)) →^* G (u), et ainsi N₁ et N₂ aura trouvé un réduit commun.

Nous allons prendre pour L le λ-calcul, dont on sait déjà qu'il est confluent; F sera défini plus loin, et G sera construit à partir de la fonction de traduction u ↦ u^* (l). Ríos utilise le sous-langage des λσ-termes σ-normaux, avec relation de réduction définie par M ⇒ N si et seulement si M se réduit par (β) en une étape en M' et N est la σ-forme normale de M'; avec comme foncteur F la fonction qui convertit tout λσ-terme en sa σ-forme normale, et G est l'inclusion canonique des termes σ-normaux dans les λσ-termes. (Dans ce dernier cas, cette méthode de preuve de confluence s'appelle la méthode d'interprétation de Hardin.)

On va commencer par donner une traduction du λσ-calcul dans le λ-calcul (le foncteur F). Comme celle du λ-calcul dans le λσ-calcul, elle prendra une liste P (de λ-termes) en argument, qui représente le contenu de la pile. La traduction M^∘(P) fabrique un λ-terme à partir d'un λσ-terme M dans une liste P, et S^∘(P) fabrique une nouvelle liste de λ-termes à partir de la pile S et de la liste P. Cette traduction n'est définie que si S est suffisamment profonde:

(MN)^∘(P)	=_def	M(P) N(P)	(λ M)^∘(P)	=_def	λ z ⋅ M^∘(z::P)
1^∘(u::P)	=_def	u	(M [S])^∘(P)	=_def	M^∘(S^∘(P))
↑^∘(u::P)	=_def	P	id^∘(P)	=_def	P
(S ∘ S')^∘(P)	=_def	S^∘(S'^∘(P))	(M ⋅ S)^∘(P)	=_def	M^∘(P) :: S^∘(P)

On vérifie que: (1) si M →_σN et M^∘(P) est défini, alors N^∘(P) est défini et M^∘(P) = N^∘(P). C'est par récurrence sur la profondeur du rédex contracté dans M. Le cas de base, où M est lui-même le rédex contracté, est une vérification longuette mais sans difficulté. Le cas le plus difficile est celui de la règle (λ), que l'on détaille comme suit:

((λ M) [S])^∘(P)	=	(λ M)^∘(S^∘(P))
	=	λ z ⋅ M^∘(z::S^∘(P))

et le côté droit:

(λ (M [1 ⋅ (S ∘ ↑)]))^∘(P)	=	λ z ⋅ (M [1 ⋅ (S ∘ ↑)])^∘(z::P)
	=	λ z ⋅ M^∘((1 ⋅ (S ∘ ↑))^∘(z::P))
	=	λ z ⋅ M^∘(1^∘(z::P) :: (S ∘ ↑)^∘(z::P))
	=	λ z ⋅ M^∘(z :: (S ∘ ↑)^∘(z::P))
	=	λ z ⋅ M^∘(z :: S^∘(↑^∘(z::P)))
	=	λ z ⋅ M^∘(z :: S^∘(P))

Ensuite, on a: (2) si M → N par la règle (β), et si M^∘(P) est défini, alors N^∘(P) aussi et M^∘ (P) →^* N^∘(P). C'est encore par récurrence structurelle sur la profondeur du rédex contracté dans M. Si cette profondeur est 0, alors M = (λ M') N', et N = M' [N' ⋅ id]. On a alors:

M^∘(P)	=	(λ M')^∘(P) N'^∘(P)
	=	(λ z ⋅ M'^∘(z::P)) N'^∘(P)
	→	M'^∘(z::P) [z:=N'^∘(P)]

Or on peut démontrer que M'^∘[u₁; …; u_n] [z:=v] = M'^∘[u₁[z:=v]; …; u_n[z:=v]], par récurrence structurelle sur M'. Comme z est fraîche, il s'ensuit que M^∘(P) → M'^∘(N'^∘(P)::P). Or on a:

N^∘(P)	=	M'^∘((N' ⋅ id)^∘(P))
	=	M'^∘(N'^∘(P) :: P)

Le cas inductif est facile. On remarquera que la traduction efface ou duplique des rédex, d'où le fait que M → N par (β) n'implique pas M^∘(P) → N^∘(P) mais M^∘(P) →^* N^∘(P).

On montre maintenant que: (3) si M^∘(P) est défini, alors (M^∘(P))^* (l) et M [P^* (l)] sont σ-convertibles, où on étend la traduction * aux listes P par [u₁; …; u_m]^* (l) =_def u₁^* (l) ⋅ … ⋅ u_m^* (l) ⋅ ↑ⁿ, où n est la longueur de l. On démontre (3) par récurrence structurelle sur M, en démontrant simultanément que (S^∘(P))^* (l) est σ-convertible avec S ∘ P^* (l) pour toute pile S.

Si M=1, alors (M^∘(P))^* (l) = u₁^* (l) où P = [u₁; …, u_m] et n≥ 1. Mais M [P^* (l)] = 1 [u₁^* (l) ⋅ … ⋅ u_m^* (l) ⋅ ↑ⁿ] → u₁^* (l).

Si M est de la forme λ M', alors (M^∘(P))^* (l) = (λ z ⋅ M'^∘(z::P))^* (l) = λ (M'^∘(z::P))^* (z::l) est σ-convertible avec λ (M' [1 ⋅ u₁^* (z::l) ⋅ … ⋅ u_m^* (z::l) ⋅ ↑ⁿ⁺¹]) par hypothèse de récurrence, si P = [u₁; …; u_m] et l est de longueur n. Or M [P^* (l)] = M [u₁^* (l) ⋅ … ⋅ u_m^* (l) ⋅ ↑ⁿ] →_σλ (M' [1 ⋅ u₁^* (l) ∘ ↑ ⋅ … ⋅ u_m^* (l) ∘ ↑ ⋅ ↑ⁿ ∘ ↑]) par (λ). Par le point (4) de la preuve du théorème 3, u_i^* (l) ∘ ↑ =_σu_i^* (z::l). Donc (M^∘(P))^* (l) =_σM [P^* (l)].

Si M est une application, c'est immédiat.

Si M est de la forme M' [S], alors (M^∘(P))^* (l) = (M'^∘(S^∘(P)))^* (l) =_σM' [(S^∘ (P))^* (l)] (par hypothèse de récurrence) =_σM' [S ∘ P^* (l)] (par hypothèse de récurrence encore) =_σM'[S] [P^* (l)] = M [P^* (l)].

Pour les piles, si S = ↑, alors en posant P = [u₁; …; u_m] et n égale la longueur de l, alors (S^∘(P))^* (l) = [u₂; …; u_m]^* (l) = u₂^* (l) ⋅ … ⋅ u_m^* (l) ⋅ ↑ⁿ, alors que S ∘ P^* (l) = ↑ ∘ (u₁^* (l) ⋅ u₂^* (l) ⋅ … ⋅ u_m^* (l) ⋅ ↑ⁿ.

Le cas S = S' ∘ S'' est similaire au cas M = M' [S]. Le cas S = id est évident, ainsi que le cas S = M ⋅ S'.

On en déduit que: (4) si M^∘[x₁; …; x_n] est défini, alors en posant l =_def [x₁; …; x_n], on a M →_σ^* (M^∘(l))^* (l). En effet, par (3) (M^∘(l))^* (l) =_σM [l^* (l)] = M [1 ⋅ … ⋅ n ⋅ ↑ⁿ] →_σM [1 ⋅ … ⋅ n−1 ⋅ ↑ⁿ⁻¹] →_σ… →_σM [1 ⋅ ↑] →_σM [id] →_σM. Ceci montre que M =_σ(M^∘(l))^* (l). Mais M^∘(l) est un λ-terme, donc le côté droit est σ-normal, d'où (4), par confluence de σ.

Supposons donc M →^* N₁ et M →^* N₂. Posons l = [x₁; …, x_n] avec n suffisamment grand pour que M^∘ (l) soit défini. Par (1) et (2), M^∘(l) se réduit en les λ-termes N₁^∘(l) et N₂^∘ (l). Mais le λ-calcul est confluent, donc il existe un λ-terme u tel que N₁^∘(l) et N₂^∘ (l) se réduisent en u. Par le théorème 3, (N_i^∘(l))^* (l) →^* u^* (l) pour chaque i ∈ {1, 2}. Mais par (4) N_i →_σ^* (N_i^∘(l))^* (l), donc N_i se réduit en u^* (l): u^* (l) est donc un réduit commun à N₁ et N₂. ♦

Exercice 14 Pour toute pile S, on pose rec (S) =_def ↑ ∘ (1 [S] ⋅ id), S₁ =_def (λ 1) 1 ⋅ id, et le duplicateur D_S (S') =_def 1 [1 [S] ⋅ S'] ⋅ S.

Montrer que S₁ ∘ S →⁺ D_S (S ∘ rec (S)) pour toute pile S. (Indication: on utilisera les règles “compliquées” (λ), (⋅), (app) de préférence aux autres, et on utilisera (β) le plus tard possible.)

Exercice 15 Posons C_S (S') =_def ↑ ∘ (1 [S'] ⋅ S). En reprenant les notations de l'exercice 14, montrer que rec (S') ∘ S →⁺ C_S (S' ∘ S) pour toutes piles S et S'.

Exercice 16 En reprenant les notations des exercices 14 et 15, montrer que, si l'on pose S_n+1 =_def rec (S_n), alors S_n ∘ S_n+1 →⁺ C_{S_n+1} (C_{S_n+1} (… C_{S_n+1} (D_{S_n+1} (S_n+1 ∘ S_n+2)) …)), où il y a n−1 opérateurs C_{S_n+1}.

En déduire que S₁ ∘ S₁ n'est pas fortement normalisant.

Exercice 17 On considère le λ-terme u =_def λ z' ⋅ (λ x ⋅ (λ y ⋅ y) ((λ z ⋅ z) x) ) ((λ y ⋅ y) z').

Montrer que u est simplement typable, donc fortement normalisant. Montrer cependant que sa traduction u^* (є) se réduit en λ (1 [S₁ ∘ S₁]) (indication: appliquer (β) en réduction externe gauche), et en déduire par les exercices précédents que u^* (є) n'est pas fortement normalisant. (On remarquera, si on est curieux, que u^* (є) est en fait typable dans les règles de typage introduites informellement au début de la section 2.2.)

Exercice 18 Démontrer que les λσ-termes et piles clos σ-normaux sont décrits par la grammaire:

N ::= N N | λ N | n

où n parcourt les entiers.

Exercice 19 En s'aidant des propriétés des traductions u ↦ u^* (l) et M ↦ M^∘(P), montrer que si u est un terme clos fortement normalisant du λ-calcul, alors u^* (l) est faiblement normalisant. Plus précisément, on montrera que si l'on pose ▷ la relation sur les λσ-termes telle que M ▷ N si et seulement si M est σ-normal, M se réduit en une étape de (β) à un terme M' et N est la σ-forme normale de M', alors u^* (l) est fortement normalisant pour ▷.

2.4 Machine à réduction pour λσ

On notera en observant la preuve du théorème 3 que u → v implique non seulement que u^* (l) se réduit en v^* (l), mais encore qu'il s'y réduit en utilisant une fois la règle (β) de β-réduction, et en normalisant ensuite par σ. Ceci correspond bien à l'idée que la normalisation par σ de M [S] effectue les substitutions représentées par la pile S. En pratique, le λσ-calcul nous laisse la possibilité de mixer β-réductions et σ-réductions. Une possibilité intéressante en pratique est de ne pas réduire les rédex (λ), autrement de ne pas faire rentrer S dans λ M par (λ). Ceci est naturel dans une stratégie de réduction faible, où de toute façon on ne réduira pas sous les λ.

On définira ainsi une machine à la Krivine pour réduire en forme normale de tête faible comme une machine à états, dont les états sont maintenant des triplets (M, S, args), où M est un terme, S la pile courante d'évaluation de M, et args la liste des termes auxquels appliquer M [S]. On obtient:

MN,	S,	args	→	M,	S,	N[S]::args
λ M,	S,	N::args	→	M,	N ⋅ S,	args
M [S'],	S,	args	→	M,	S' ∘ S,	args

où l'on restreint M à ne pas être de la forme n ou x ou x [↑ⁿ], n≥ 1 dans la dernière règle. On complète ceci par une série de règles ayant pour but de normaliser les substitutions, lorsque le terme est de la forme n ou x ou x [↑ⁿ] (par convention on écrira x [↑⁰] = x):

1,	N ⋅ S,	args	→	N,	id,	args
n+1,	N ⋅ S,	args	→	n,	S,	args
x [↑ⁿ⁺¹],	N ⋅ S,	args	→	x [↑ⁿ]	S,	args
n,	↑,	args	→	n+1,	id,	args
x [↑ⁿ],	↑,	args	→	x [↑ⁿ⁺¹],	id,	args
n,	↑ ∘ S,	args	→	n+1,	S,	args
x [↑ⁿ],	↑ ∘ S,	args	→	x [↑ⁿ⁺¹],	S,	args
M,	id ∘ S,	args	→	M,	S,	args
M,	(S'' ∘ S') ∘ S,	args	→	M,	S'' ∘ (S' ∘ S),	args
M,	(N ⋅ S') ∘ S,	args	→	M,	N[S] ⋅ (S' ∘ S),	args

où M est de la forme n ou x [↑ⁿ].

Noter que la règle qui s'applique quand le terme est de la forme λ M correspond à la règle (λ M) [S] N → λ (M [1 ⋅ (S ∘ ↑)]) N → M [1 ⋅ (S ∘ ↑)] [N ⋅ id] → M [(1 ⋅ (S ∘ ↑)) ∘ (N ⋅ id)] →^* M [N ⋅ S]. Il n'y a pas de règle pour les termes de la forme λ M lorsque la liste d'arguments est vide: c'est ce qui représente le fait qu'on ne propage pas réellement les substitutions sous les λ. Si on voulait le faire, il faudrait ajouter la règle:

λ M,

[]

→

λ M,

1 ⋅ S ∘ ↑,

[]

Noter aussi qu'aucune règle ne réduit spontanément la pile S, sauf lorsque le terme est de la forme n ou x ou x [↑ⁿ].

Exercice 20 Montrer que si M, S, [M₁; …; M_n] →^* M', S', [M'₁; …; M'_n'] dans la machine ci-dessus, alors M [S] M₁ … M_n est σ-convertible avec un terme qui se réduit dans le λσ-calcul à un terme σ-convertible avec M' [S'] M'₁ … M'_n'.

Exercice 21 Montrer que dans le cas semi-clos, si la machine ci-dessus termine, alors c'est dans un état de la forme M, id, args où M est de la forme n, x, ou x [↑ⁿ], ou λ M'.

Exercice 22 Une forme normale de tête faible en λσ-calcul est un terme de la forme λ M, ou bien h M₁ … M_n, où la tête h est de la forme n ou x ou x [↑ⁿ]. Montrer que la machine ci-dessus calcule une forme normale de tête faible d'un λσ-terme semi-clos M s'il en a une, en démarrant de l'état M, id, []. (On utilisera la traduction M ↦ M^∘(l) pour l suffisamment grande et ses propriétés, le théorème de standardisation du λ-calcul, et l'exercice 20.)