

1 Logique combinatoire
Le problème que nous cherchons à traiter dans ce chapitre est le
suivant: nous souhaitons écrire un programme qui prend un
λ-terme en entrée et retourne sa forme normale, si elle
existe.
Le premier point que nous devrons traiter est la représentation
des λ-termes. Une idée est d'utiliser une structure
d'arbre, correspondant au type Caml:
type lambda_terme = VAR of string (* variables nommees *)
| APPL of lambda_terme * lambda_terme (* applications *)
| ABS of string * lambda_terme;; (* abstractions *)
Ceci est cependant assez maladroit, comme le lecteur pourra s'en
apercevoir s'il essaie d'écrire une fonction de réduction pour
ce langage. Essayons de le faire: nous voulons écrire une
fonction norm : lambda_terme -> lambda_terme qui normalise
son terme d'entrée. Nous connaissons déjà une stratégie qui
atteint ce but: la stratégie externe gauche. Utilisons-la:
let rec norm t =
match t with
VAR x -> t (* une variable est normale. *)
| ABS (x, u) -> ABS (x, norm u) (* normaliser une abstraction
revient a normaliser son corps. *)
| APPL (u, v) ->
let u' = norm u in (* strategie gauche : reduire
les redex de u avant ceux de v. *)
match u' with
ABS (y, u1) -> norm (subst u1 y v) (* beta-reduction *)
| _ -> APPL (u', norm v);;
Il ne reste qu'à définir une fonction subst de
substitution: ceci n'est pas trivial, à cause des problèmes
particuliers posés par la capture de variables et le
α-renommages. De plus, la complexité de subst u1 y v, si elle est en temps polynomial en u1,
est néanmoins élevée: à chaque β-réduction, le term
u1 doit être parcouru en entier. Ensuite, alors que
u1 est déjà en forme normale dans le cas APPL (u, v), l'appel récursif à norm (subst u1 y v) va re-parcourir u1 avant de tomber
sur les rédex dans v ou ceux créés par la substitution.
Un tel re-parcours est coûteux lui aussi. Enfin, peut-on garantir
que la fonction norm est correcte ?
1.1 Combinateurs SKI
Une idée qui résout la plupart de ces problèmes est due
originellement à Schönfinkel et à Curry, c'est la logique
combinatoire. Le principe essentiel derrière la logique
combinatoire est d'éliminer les variables et les abstractions du
langage, et de compiler les λ-termes vers un langage simple,
du premier ordre, n'ayant que l'application comme symbole de
fonction, toutes les autres constructions élémentaires étant
codées via un certain nombre de constantes appelées combinateurs.
Que ceci soit faisable est surprenant. Essayons de voir comment on
peut définir λ x ⋅ u à β-équivalence près,
en utilisant quelques λ-termes clos prédéfinis. Ceci se
fait par récurrence structurelle sur u. Si u est une
variable, soit u=x et on prédéfinit I =def λ x ⋅ x
(l'identité); soit u est une autre variable y, et alors
λ x ⋅ y =βKy, où K =def λ y,x ⋅ y est
notre deuxième λ-terme clos prédéfini. Si u est une
application vw, alors λ x ⋅ vw =βλ z ⋅
(λ x ⋅ v) z ((λ x ⋅ w) z) =βS (λ x
⋅ v) (λ x ⋅ w), où S =def λ x, y, z ⋅ xz
(yz) est notre troisième λ-terme clos prédéfini.
Finalement, si u est une abstraction, on peut supposer que cette
abstraction a été éliminée préalablement en faveur des
constantes S, K, I ci-dessus, et on n'a donc rien de plus à
faire — à part déclarer que λ x ⋅ S =βKS,
λ x ⋅ K =βKK, λ x ⋅ I =βKI.
Formalisons cette idée. Le langage des combinateurs de
Curry est:
TCurry ::= V | TCurry TCurry
| S | K | I
Pour les distinguer des λ-termes, notons les termes, ou
combinateurs de Curry à l'aide des lettres M, N, P, etc. Ce
langage est muni de la relation de réduction:
|
|
| S M N P |
→ |
MP(NP) |
| K M N |
→ |
M |
| I M |
→ |
M |
|
et on compile les λ-termes en combinateurs par la
transformation u ↦ u* suivante, où la compilation
d'abstractions λ x ⋅ u est exprimée sous forme d'une
opération d'abstraction [x] M prenant un terme M de
TCurry et retournant un autre terme de Curry,
suivant l'explication donnée plus haut. (Noter que [x] n'est
pas un symbole du langage, mais un opérateur envoyant des termes
de Curry vers des termes de Curry.)
|
|
| x* |
=def |
x |
| (uv)* |
=def |
u* v* |
| (λ x ⋅ u)* |
=def |
[x] (u*) |
|
|
| [x] x |
=def |
I |
| [x] y |
=def |
K y (y≠ x) |
| [x] a |
=def |
K a (a ∈ {S, K, I}) |
| [x] (MN) |
=def |
S ([x] M) ([x] N) |
|
Les combinateurs formalisent bien la notion de β-réduction,
en tout cas à première vue:
Lemme 1
Pour tous termes de Curry M et N, ([x] M) N →* M [x:=N].
Preuve :
Par récurrence structurelle sur M. Si M=x, alors ([x] M) N
= I N → N = M [x:=N]. Si M est une autre variable y ou
une constante a ∈ {S, K, I}, alors ([x] M) N = K M
N → M = M [x:=N]. Si M est une application M1 M2, alors
([x] M1 M2) N = S ([x] M1) ([x] M2) N → ([x] M1) N (([x]
M2) N) →* M1 [x:=N] (M2 [x:=N]) (par hypothèse de
récurrence) = M [x:=N].
♦
On peut alors réaliser une fonction ski_norm de termes de
Curry plus simplement que dans le cas du λ-calcul, comme
suit:
type ski_terme = S | K | I
| VAR of string
| APPL of ski_terme * ski_terme;;
let rec ski_norm m =
match m with
S | K | I -> m
| VAR x -> m
| APPL (m0, m1) ->
match ski_norm m0 with
I -> ski_norm m1
| APPL (K, m') -> m'
| APPL (APPL (S, m3), m2) -> ski_norm (APPL (APPL (m3, m1), APPL (m2, m1)))
| m'0 -> APPL (m'0, ski_norm m1);;
La fonction ski_norm effectue une réduction externe gauche.
L'exercice 4 permet de montrer qu'il s'agit d'une
stratégie de réduction, au sens ou si le terme donné en
argument à ski_norm a une forme normale, alors
ski_norm termine et retourne une forme normale. De plus, le
système de combinateurs de Curry est confluent
(exercice 5), et donc ski_norm retourne
l'unique forme normale du terme en entrée si elle existe.
La fonction ski_norm a cependant toujours le défaut qu'elle
reparcourt les termes plusieurs fois. Par exemple, pour normaliser
S x y z, ski_norm descend le long de ce dernier,
normalise S, normalise x, retourne S x (dernière ligne);
puis normalise y, retourne S x y. À ce stade,
ski_norm appliqué à S x y z a obtenu m0=def
S x y comme forme normale de S x y et m1=def z. On
tombe alors dans le troisième cas du match ski_norm m0
ci-dessus, qui demande à normaliser xz(yz). De nouveau,
ski_norm va s'appeler récursivement sur xz, puis sur x,
puis remonter et finir par conclure que le terme est en forme
normale.
Pour éviter ce problème, on peut utiliser l'astuce de
Krivine, qui consiste à faire de ski_norm une fonction
binaire, qui prend non seulement un terme M à normaliser, mais
aussi une liste [M1, …, Mn] d'arguments auxquels appliquer
M. On définit donc:
let rec ski_norm m args =
match m with
APPL (m0, m1) -> ski_norm m0 (m1::args) (* on accumule les arguments. *)
| I -> (match args with
[] -> I (* I applique a rien. *)
| m1::rest -> ski_norm m1 rest (* I m1 ... -> m1 ... *))
| K -> (match args with
m1::m2::rest -> ski_norm m1 rest (* K m1 m2 ... -> m1 ... *)
| _ -> hnf m args)
| S -> (match args with
m1::m2::m3::rest -> ski_norm m1 (m3::APPL(m2,m3)::rest)
(* S m1 m2 m3 ... -> m1 m3 (m2 m3) ... *)
| _ -> hnf m args)
| VAR _ -> (* x m1 ... mn est normal de tete: on le reconstruit,
en appelant recursivement ski_norm sur les arguments
m1, ..., mn. *)
hnf m args
and hnf m args = (* applique m a args, en evaluant recursivement les args. *)
match args with
[] -> m
| arg::rest -> hnf (APPL (m, ski_norm arg [])) rest;;
Cette fonction effectue une normalisation par stratégie externe
gauche. Si l'on souhaite effectuer une normalisation de tête
seulement, c'est-à-dire ne pas normaliser les arguments m1,
..., mn lorsqu'on évalue une forme normale de tête m m1
… mn, il suffit de réécrire la définition de hnf
en:
and hnf m args = (* applique m a args, en evaluant recursivement les args. *)
match args with
[] -> m
| arg::rest -> hnf (APPL (m, arg)) rest
in hnf m args;;
On notera au passage que ski_norm et hnf sont alors
des fonctions récursives en queue (en anglais, tail-recursive), autrement dit quand on récurse sur
ski_norm ou hnf, c'est pour obtenir un résultat
qu'on se contentera de retourner directement. (Noter qu'il est
important de ne faire que de la réduction de tête pour
obtenir un tel résultat.) Un tel appel d'une fonction f dont le
résultat sera retourné de la fonction courante est un appel
en queue. Si vous avez quelques notions d'assembleur, vous vous
convaincrez facilement qu'un appel en queue peut être simulé par
un goto pointant vers le début du code de la fonction f.
Si vous connaissez C, vous verrez au moins qu'un appel récursif en
queue de f (dans le code de f, donc), peut être simulé par
un goto retournant au début de la fonction. Par exemple,
la fonction hnf ci-dessus peut être codée en C par:
ski_terme hnf (ski_terme m, ski_terme_liste args) {
while (m!=nil) {
m = APPL (m, hd (args));
args = tl (args);
}
return m;
}
où nil est la liste vide, hd récupère le premier
élément d'une liste non-nil et tl récupère la
queue de cette même liste, et APPL construit une
application comme en Caml. Les types ski_terme et
ski_terme_liste pourront être définis comme suit:
typedef struct skit {
int kind; /* -1=VAR, 0=I, 1=K, 2=S, 3=APPL */
union {
char *var; /* lorsque kind==-1. */
struct appl { struct skit *f, *arg; } appl; /* lorsque kind==3. */
} what;
} skit, *ski_terme;
typedef struct skitl {
ski_terme hd; /* liste non vide; la liste vide nil est NULL. */
struct skitl *tl;
} skitl, *ski_terme_liste;
La conséquence majeure de l'astuce de Krivine est qu'on obtient un
évaluateur de termes de Curry non récursif pour la
réduction de tête, qui ne consomme donc aucune place dans la
pile du processeur. Bien sûr, cette pile est en un sens simulée
par la liste args des arguments en attente d'évaluation,
mais on n'a par exemple pas besoin de garder (comme en C, par
exemple), une pile contenant les addresses de retour des
sous-programmes appelés. Ceci est une particularité de l'appel
par nom. L'appel par valeur, en revanche, ne permet pas
l'évaluation sans pile.
On écrira l'évaluateur de Krivine sous forme symbolique, à
l'aide de règles de transition entre états machine. Un état est ici un couple (M, args), où M est un terme et
args une liste d'arguments:
|
|
| M0 M1, |
args |
→ |
M0, |
M1::args |
| I, |
M::args |
→ |
M, |
args |
| K, |
M1::M2::args |
→ |
M1, |
args |
| S, |
M1::M2::M3::args |
→ |
M1, |
M3::M2 M3::args |
|
Lorsque ce système termine sur un état (M, [M1; …;
Mn]), c'est qu'on a trouvé la forme normale de tête faible M
M1 … Mn.
Exercice 1
Écrire la fonction ski_norm en C en profitant de la
récursion en queue.
Exercice 2
Justifier le fait que la réduction appelée réduction de
tête ci-dessus est bien nommée. On remarquera que cette
réduction est la relation binaire (ne passant pas au contexte)
définie par:
|
|
| I M1 M2 … Mn |
→ |
M1 M2 … Mn (n≥ 1) |
| K M1 M2 M3 … Mn |
→ |
M1 M3 … Mn (n≥ 2) |
| S M1 M2 M3 M4 … Mn |
→ |
M1 M3 (M2 M3) M4 … Mn (n≥ 3) |
|
Exercice 3
Calculer (λ x, y ⋅ x)*. Ce terme est-il égal
à, ou se réduit-il à K?
Exercice 4
Remarquer que tout terme de Curry s'écrit de façon unique
sous la forme h M1 … Mn, où h, la tête
du
terme, est une variable ou un combinateur parmi S, K,
I. On définit la relation de réduction de tête
par I M1 M2 … Mn →t M1 M2 … Mn si n ≥
1, K M1 M2 M3 … Mn → M1 M3 … Mn si n ≥
2, S M1 M2 M3 M4 … Mn → M1 M3 (M2 M3) M4
… Mn si n ≥ 3. Notons →r* sa clôture
réflexive transitive. Comme dans le λ-calcul, on
définit la relation →s* de réduction standard
en
posant que M →s* N si et seulement si M →r* h M1
… Mn, M1 →s* N1, ..., Mn →s* Nn, et N =
h N1 … Nn. (Ceci est une définition par récurrence
structurelle sur N.)
Montrer que si M →s* N → P, alors M →s* P. (On
pourra s'inspirer de la preuve du théorème de standardisation
en partie 1.) En déduire le théorème de standardisation
pour le calcul des combinateurs de Curry.
Exercice 5
On définit une notion de réduction parallèle ⇒
par:

Montrer que ⇒ est fortement confluente. Montrer
d'autre part que si M → M' alors M ⇒ M', et si M
⇒ M' alors M →* M'. En déduire que la notion de
réduction des termes de Curry est confluente.
Jusqu'ici, tout semble parfait. Mais les combinateurs de Curry ne
sont pas si parfaits que cela. En premier, le
lemme 1 ne suffit pas: ce n'est pas parce que
([x] M) N →* M [x:= N] que la réduction des combinateurs
permet de simuler la β-réduction du λ-calcul (via la
traduction u ↦ u*). Ceci peut paraîitre surprenant,
mais la propriété qu'on aimerait avoir est le fait que pour tous
λ-termes u et v, ((λ x ⋅ u) v)* →* (u
[x:=v])*, c'est-à-dire ([x] u*) v* →* (u [x:=v])*.
Or si le côté gauche se réduit bien en u* [x:=v*] par le
lemme 1, rien ne permet d'assurer que u*
[x:=v*] soit égal, ou même se réduise en (u [x:=v])*.
En fait, dans notre traduction u ↦ u*, en général u*
[x:=v*] et (u [x:=v])* ne sont même pas convertibles.
Considérer par exemple u =def λ y ⋅ x, v =def zz'. On
a u* = K x, v* = zz', donc u* [x:=v*] = K (zz'), mais
(u [x:=v])* = (λ y ⋅ zz')* = [y] (zz') = S (K
z) (K z'), et ces deux termes sont différents et normaux.
Comme le calcul est confluent (exercise 5), ces deux
termes ne sont même pas convertibles. Ce défaut est cependant
relativement aisé à corriger: voir
l'exercice 6.
Exercice 6
On définit la traduction u ↦ uβ suivante, qui est
une variation mineure de la traduction u ↦ u*, comme
suit:
|
|
| xβ |
=def |
x |
| (uv)β |
=def |
uβ vβ |
| (λ x ⋅ u)β |
=def |
[x]β(uβ) |
|
|
| [x]βx |
=def |
I |
| [x]βM |
=def |
K M (x ∉fv(M)) |
| [x]β(MN) |
=def |
S ([x]βM) ([x]βN) (x ∈ fv(MN)) |
|
Même en effectuant la réparation de
l'exercice 6, ce qu'on veut vraiment c'est que si u
→ v par β-réduction, alors uβ →* vβ. Il
faut donc vérifier que si M → M' alors MN → M'N (trivial),
que si N → N' alors MN → MN' (trivial), et que si M → M'
alors [x]βM →* [x]βM'. Cette dernière
implication est connue sous le nom de règle (ξ), et
malheureusement elle n'est pas vraie.
Considérons par exemple M =def ([y]βz) x = K z x et M'
=def z. Alors M → M', mais [z]βM = S (S (K K)
I) (K x) est normal, et ne se réduit donc pas à [z]β M' = I. Noter que ça ne fonctionnerait pas non plus avec
([y] z) x au lieu de ([y]βz) x, qui est en fait le même
terme.
En fait, on ne connaît aucune traduction f des λ-termes vers
les termes de Curry telle que u =βv si et seulement si f
(u) et f (v) sont convertibles par les règles de réduction
des combinateurs. On vient de voir que les traductions u ↦
u* et u ↦ uβ n'avaient pas cette propriété, mais
aucune autre traduction connue ne l'a.
Toute ceci est gênant dans une optique où l'on implémenterait
un assistant de preuve comme Coq [BBC+99], qui fait un usage
essentiel du λ-calcul et de la relation de
β-convertibilité, mais l'est moins dans le cas de la
réalisation d'un langage de programmation.
Dans ce dernier cas, et en laissant de côté le fait que les
notions de réduction qui nous intéressent dans ce cas sont
plutôt des réductions de tête faibles, ce que l'on souhaite
faire, c'est traduire un λ-terme u en un terme de Curry
M, typiquement uβ, réduire M en une forme normale N,
puis retraduire N en un λ-terme que l'on imprimera. La
traduction naïve M ↦ M∘ des termes de Curry en
λ-termes est:
|
|
| x∘ |
=def |
x |
| (MN)∘ |
=def |
M∘N∘ |
| I∘ |
=def |
λ x ⋅ x |
| K∘ |
=def |
λ x, y ⋅ x |
| S∘ |
=def |
λ x, y, z ⋅ xz(yz) |
|
Il s'agit bien d'une traduction inverse, mais seulement à
β-équivalence près, au sens où:
Lemme 2
Pour tout λ-terme u, (u*)∘→* u.
Preuve :
Par récurrence structurelle sur u. Le seul cas non trivial
est celui des abstractions u =def λ x ⋅ v, où l'on
doit montrer que ([x] v*)∘=βλ x ⋅ v.
Ceci étant une conséquence de l'hypothèse de récurrence
(v*)∘=βv et du fait que ([x] M)∘=β λ x ⋅ M∘, il ne reste qu'à démontrer cette
dernière égalité. Ceci est par récurrence structurelle
sur M: si M = x, alors ([x] M)∘= I∘= λ
x ⋅ x = λ x ⋅ M∘; si M est une autre
variable y, alors ([x] M)∘= (K y)∘= (λ
x,x' ⋅ x) y → λ x' ⋅ y = λ x ⋅ M∘;
si M est une application, c'est trivial; si M = I, alors
([x] M)∘= (K I)∘= (λ y, x ⋅ y)
(λ z ⋅ z) → λ x, z ⋅ z = λ x ⋅
M∘; si M = K, alors ([x] M)∘= (K K)∘ = (λ y, x ⋅ y) (λ z, z' ⋅ z) → λ x, z,
z' ⋅ z = λ x ⋅ M∘; si M = S, alors ([x]
M)∘= (K S)∘= (λ y, x ⋅ y) (λ
z, z', z'' ⋅ zz''(z'z'')) → λ x, z, z', z'' ⋅
zz''(z'z'') = λ x ⋅ M∘.
♦
Mais ce n'est pas satisfaisant, car M∘ n'est pas en
général un terme normal dans le λ-calcul, même si M
est un terme de Curry normal. Par exemple, si M = K x, on a
M∘= (λ x, y ⋅ x) x, et bien sûr la traduction
inverse λ y ⋅ x aurait été préférable. Or
obtenir ce dernier à partir du précédent revient à effectuer
une série de β-réductions, ce qui est justement ce pour
quoi on avait cherché à traduire nos λ-termes en
combinateurs au départ...
Il y a beaucoup de systèmes de combinateurs, et le livre
[Dil88] en donne un panorama assez exhaustif, en passant
par les supercombinateurs et les combinateurs catégoriques
notamment. Nous verrons ces derniers en filigrane en
section 2, puisque les λ-calculs à
substitutions explicites y trouvent leur source.
Exercice 7
Montrer que (u∘)* et u ne sont même pas convertibles
en général. (Prendre M =def K.) Qu'en est-il de
(u∘)β et u ?
Exercice 8
Montrer que si M et N sont convertibles en temps que termes de
Curry, alors M∘=βN∘.
Exercice 9
Montrer qu'on pouvait se passer du combinateur I dans la
définition des termes de Curry, au sens où le fait de poser
I =def S K N (pour n'importe quel terme N) permet de
réduire I M en M.
Exercice 10
La discipline de types simples naturelle des combinateurs est
héritée du λ-calcul. On a une règle de typage:

un axiome logique Γ, x : F ⊢ x : F, et trois
axiomes Γ ⊢ I : F ⇒ F, Γ ⊢ K
: F1 ⇒ F2 ⇒ F1, Γ ⊢ S : (F1
⇒ F2 ⇒ F3) ⇒ (F1 ⇒ F2) ⇒
F1 ⇒ F3. Déduire de ces considérations et de
l'isomorphisme de Curry-Howard qu'une formule F est
déductible en logique intuitionniste minimale propositionnelle
si et seulement si elle est déductible dans le système
ci-dessus (qui n'a pas la règle d'introduction de
l'implication). Montrer en fait que la règle d'introduction de
l'implication est réalisée par l'abstraction, au sens où
Γ, x : F1 ⊢ M : F2 implique Γ ⊢ [x]
M : F1 ⇒ F2 (resp. Γ ⊢ [x]βM :
F1 ⇒ F2).
Exercice 11
Montrer que tout terme de Curry typable est fortement normalisant.
On s'inspirera de la méthode de réductibilité, en
simplifiant légèrement l'argument: montrer les conditions
(CR1), (CR2) et (CR3) (on dira qu'un terme est neutre
s'il
n'est pas de la forme I ou K ou K M ou S ou S
M ou S M N); montrer ensuite directement par récurrence
structurelle sur M que si Γ ⊢ M : F alors M est
réductible de type F.
1.2 Machines à réduction de graphes
La machine ski_norm a toujours le défaut qu'ont toutes les
machines à réduction par nom, à savoir que si dans u la
variable x apparaît libre plusieurs fois, disons n, alors
dans la réduction de (λ x⋅ u) v en u [x:=v], la
valeur de v sera recalculée n fois.
Par exemple, (λ x ⋅ xx) v se réduit par nom en vv,
et si on suppose que la forme normale de v est v' et que v'
est neutre (pas une abstraction), alors vv se réduit en v'v,
puis seulement en v'v'. L'interprète ski_norm fait
pareil: la traduction de (λ x ⋅ xx) v est S I I
vβ, qui se réduit en I vβ(I vβ), puis en
vβ(I vβ). Ceci se réduit en M (I vβ),
où M est la forme normale de vβ, puis en MM. Mais pour
cela, on a du réduire vβ deux fois à sa forme normale.
Pour éviter ceci, on peut représenter les termes de Curry sous
forme non pas d'arbres mais de graphes, de sorte à conserver le
partage. Graphiquement, les règles de réduction seront:
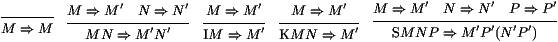 où l'argument P est bien partagé dans la dernière règle.
où l'argument P est bien partagé dans la dernière règle.
Ce qui est important, au passage, ce n'est pas tant de partager les
sous-termes tels que P, mais que toute réduction dans P ne
soit effectuée qu'une fois. Autrement dit, une fois P
évalué, on doit remplacer P par sa valeur, en
utilisant un effet de bord.
Concrètement, le type des graphes représentant des termes sera:
type ski_graphe = S | K | I
| VAR of string
| APPL of ski_graphe ref * ski_graphe ref;;
et la fonction de normalisation ski_norm (sans astuce de
Krivine) va devoir être adaptée pour mémoriser les calculs en
transformant le graphe représentant un terme au fur et à mesure.
On définit ainsi la fonction ski_gnorm de type
ski_graphe ref→unit, qui modifie physiquement le
graphe fourni en entrée. On peut ensuite lire la forme normale en
déréférençant le graphe de départ.
let rec ski_gnorm p =
match !p with
APPL (p0, p1) ->
(ski_gnorm p0;
match !p0 with
I -> (p:=!p1; ski_gnorm p) (* on remplace I p1 par p1 physiquement et on recurse. *)
| APPL ({contents=K}, {contents=m'}) -> (p:=m'; ski_gnorm p)
| APPL ({contents=APPL ({contents=S}, p3)}, p2) ->
(p:=APPL (ref (APPL (p3, p1)), ref (APPL (p2, p1)));
ski_gnorm p)
| _ -> ski_gnorm p1 (* on normalise l'argument *) )
| _ -> ();;
Exercice 12
On ajoute au langage un combinateur Y de point fixe primitif, de
règle de réduction Y M → M (YM). Modifier
ski_graphe et la machine ski_gnorm pour intégrer
ce nouvel opérateur. En quoi l'utilisation de graphes est-elle
ici particulièrement utile ?







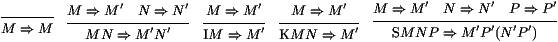 où l'argument P est bien partagé dans la dernière règle.
où l'argument P est bien partagé dans la dernière règle.
