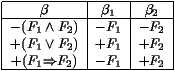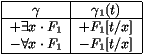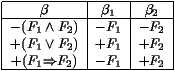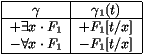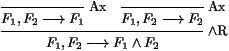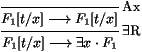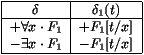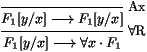Une tentative presque réussie

1 Une tentative presque réussie

Nous pouvons voir tout séquent F₁, ..., F_m ¾® G₁, ..., G_n comme un ensemble -F₁, ..., -F_m, +G₁, ..., +G_n de formules signées (une branche de tableaux). Nous dirons qu'une branche -F₁, ..., -F_m, +G₁, ..., +G_n est cohérente si et seulement si le séquent correspondant F₁, ..., F_m ¾® G₁, ..., G_n est improuvable. Ceci signifie que l'on peut supposer que toutes les formules négatives sont vraies et toutes les formules positives sont fausses, sans que le système de déduction puisse en déduire le faux (le séquent vide).

En général, nous allons considérer des branches B infinies. Nous dirons alors que B est cohérente si et seulement si toute sous-branche finie est cohérente.

Nous observons d'abord que :

Lemme 1   Pour toute branche cohérente B, il existe une branche cohérente maximale B_¥ contenant B.
Preuve : C'est une application du lemme de Zorn (une variante de l'axiome du choix) : tout ensemble ordonné inductif a un élément maximal. Rappelons qu'un ensemble ordonné (E, £) est dit inductif si et seulement si toute famille totalement ordonnée (x_i)_{iÎ
I} d'éléments de E a un majorant. La famille (x_i)_{iÎ I} est totalement ordonnée si et seulement si pour tous i, j Î I, x_i £ x_j ou x_j £ x_i. Un élément maximal d'un ensemble est un élément de l'ensemble qui est ³ à tous les éléments de l'ensemble.

Considérons l'ensemble E de toutes les branches cohérentes contenant B, ordonné par l'inclusion. Si (B_i)_{iÎ I} est une famille totalement ordonnée d'éléments de E, considérons B' = È_{iÎ I} B_i. B' est clairement un majorant des B_i, et nous prétendons que B' est dans E, c'est-à-dire que toute sous-branche finie B'' de B' est cohérente. Or B'' étant finie, est incluse dans une union finie des B_i et donc dans l'un des B_i, puisque la famille est totalement ordonnée. Mais B_i étant cohérente, et B'' étant une sous-branche de B_i, B'' est nécessairement cohérente. Comme B'' est une sous-branche arbitraire de B', B' est cohérente. Il ne reste qu'à appliquer le lemme de Zorn, et à choisir pour B_¥ un élément maximal quelconque de E. ¤

Les branches cohérentes maximales ont des propriétés remarquables :

Lemme 2   Pour toute branche cohérente maximale B, pour toute formule F, soit +F soit -F est dans B.
Preuve : Clairement, +F et -F ne peuvent pas être toutes les deux dans B, sinon B ne serait pas cohérente. Réciproquement, supposons que ni +F ni -F ne soit dans B. Comme B est maximale, ceci signifie que B È {+F} et B È {-F} sont toutes les deux incohérentes. Donc il existe des sous-ensembles finis B₁ et B₂ de B È {+F} et B È {-F} respectivement, qui, vus comme des séquents, sont prouvables. On peut sans perte de généralité supposer que +F Î B₁ et -F Î B₂, car l'affaiblissement est admissible en LK. Posons alors B'₁ = B₁ \ {+F}, B'₂ = B₂ \ {-F}. Par une application de la règle de coupure sur F, on en déduit une preuve de B'₁ È B'₂. Mais par construction B'₁ et B'₂ sont des sous-ensembles de B, donc B'₁ È B'₂ aussi : nous venons de démontrer que B était incohérent, ce qui est impossible par hypothèse. Donc +F ou -F doit appartenir à B. ¤

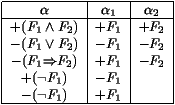
Lemme 3   Pour toute branche cohérente maximale B :

si a est une formule comme suit dans B, alors l'une des formules signées correspondantes a₁ ou a₂ est aussi dans S :
si b est une formule comme suit dans B, alors les formules signées correspondantes b₁ et b₂ sont aussi dans B :
si g est une formule comme suit dans B, alors pour tout terme t, la formule correspondante g₁ (t) est dans S :

Preuve : a : si + (F₁ Ù F₂) est dans B, mais que ni +F₁ ni +F₂ ne sont dans B, alors par le lemme 2, -F₁ et -F₂ sont dans B. Mais la sous-branche -F₁, -F₂, +(F₁ Ù F₂) est incohérente, puisqu'on a la preuve :

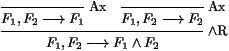
Ceci implique que B elle-même est incohérente, ce qui est absurde.

Les autres cas de règles a se démontrent de façon similaire, en utilisant les règles ÚL, ÞL, ¬R et ¬L respectivement.

b : de même, en utilisant les règles ÙL, ÚR, ÞR.

g : supposons que +$ x · F₁ soit dans B mais pas +F₁ [t/x], où t est un terme quelconque donné. Par le lemme 2, -F₁ [t/x] est dans B, mais ceci est contredit par le fait que l'on peut prouver :

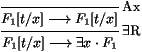
De même pour -" x· F₁, en utilisant "L. ¤

Nous aimerions bien avoir aussi la propriété :

4. si d est une formule comme suit dans B, alors il existe un terme t tel que la formule correspondante d₁ (t) soit dans B :

La preuve serait : supposons que +" x · F₁ soit dans B, mais que +F₁ [t/x] ne soit pas dans B pour aucun terme t. En particulier, +F₁ [y/x] n'est pas dans B, où y est une variable non libre dans " x · F₁; donc -F₁ [y/x] est dans B par le lemme 2. Un raisonnement (trop) rapide permettrait de contredire la cohérence de B, observant que l'on peut dériver :

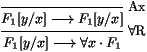
Mais cet argument ne fonctionne pas, parce que pour appliquer "R, il faudrait que y ne soit pas libre dans le F₁ [y/x] du côté gauche, ce qui est en général impossible.

Ignorons le problème pour l'instant, et définissons :

Définition 4   Une branche B est appelée saturée si et seulement si elle vérifie les propriétés 1.--4.

Lemme 5   On dit que I, r falsifie +F si et seulement si non I, r |= F; I, r falsifie -F si et seulement si I, r |= F. I, r falsifie un ensemble de formules signées B si et seulement si I, r falsifie tous les éléments de B. On dit alors que (I, r) est un contre-modèle de B.

Soit B une branche maximale cohérente, et supposons B saturée. Alors B a un contre-modèle.
Preuve : Définissons le comme un modèle à la Herbrand. Le domaine D de l'interprétation est l'ensemble de tous les termes, et pour chaque symbole de fonction f d'arité n, l'interprétation I (f) est la fonction qui aux termes t₁, ..., t_n associe le terme f (t₁, ..., t_n). Pour chaque symbole de prédicat P d'arité n, posons I (P) la fonction qui à t₁, ..., t_n associe vrai si et seulement si -P (t₁, ..., t_n) est dans B. Notons que : (a) pour toute affectation r (qui est en même temps une substitution), pour tout terme t, [t] I r = t r. C'est une récurrence facile sur t.

Soit enfin r l'affectation qui à toute variable x associe le terme x dans D. Notons que, pour toute formule atomique A, on a I, r |= A si et seulement si -A Î B : en effet, soit A = P (t₁, ..., t_n), alors I, r |= A si et seulement si -P ([t₁] I r, ..., [t_n] I r) Î B, c'est-à-dire, en utilisant (a), si et seulement si -P (t₁, ..., t_n) Î B, autrement dit si et seulement si -A Î B.

Nous montrons que I, r falsifie toute formule signée ± F de B, par récurrence structurelle sur F. Si F est une formule atomique A, c'est par construction : si -A est dans B, alors par définition I, r |= A; et si +A est dans B, alors non I, r |= A, car sinon -A serait aussi dans B, ce qui contredirait la cohérence de B.

Si ± F est une formule a, par exemple + (F₁ Ù F₂), alors comme la branche est saturée, +F₁ ou +F₂ est aussi dans B, donc par hypothèse de récurrence I, r falsifie +F₁ ou +F₂. Dans chaque cas, I, r doit donc falsifier + (F₁ Ù F₂). Le raisonnement est similaire dans le cas des autres formules a, ainsi que pour les formules b.

Si ± F est une formule g, par exemple +$ x · F₁, alors parce que la branche est saturée, pour tout terme t, +F₁ [t/x] est dans B. Par hypothèse de récurrence, I, r falsifie +F₁ [t/x]; mais si on avait I, r |= $ x · F₁, alors il existerait une valeur pour x rendant F₁ vraie dans I, r. Une telle valeur est par définition un terme t, et donc on aurait I, r |= F₁ [t/x], ce qui est impossible. Donc I, r falsifie +$ x · F₁. Le cas de -" x · F₁ est similaire.

Si ± F est une formule d, par exemple +" x · F₁, alors puisque la branche est saturée, il existe un terme t tel que +F₁ [t/x] soit dans B. Par hypothèse de récurrence, I, r falsifie F₁ [t/x]; mais si on avait I, r |= " x · F₁, alors en particulier I, r [t/x] |= F₁, et donc I, r |= F₁ [t/x]. Donc I, r falsifie +" x · F₁. Le cas de -$ x · F₁ est similaire. ¤

Nous en déduisons immédiatement :

Théorème 6   Supposons que toute branche cohérente finie B soit incluse dans une branche cohérente maximale B_¥ qui est saturée.

Alors LK est complet : tout séquent valide est prouvable.
Preuve : Soit B un séquent, vu comme une branche finie, et supposons par l'absurde que B ne soit pas prouvable, autrement dit que B soit cohérente. Par hypothèse, il existe une branche cohérente maximale B_¥ contenant B, et qui est saturée. Par le lemme 5, B_¥ a un contre-modèle, donc B aussi, ce qui contredit la validité de B. ¤

Mais comme toute branche cohérente maximale n'est pas nécessairement saturée (la propriété 4. peut échouer), la construction d'une branche B_¥ comme au lemme 1 ne suffit pas pour garantir que B_¥ soit saturée.