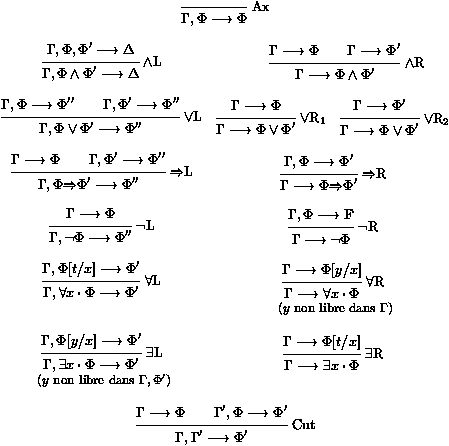
Figure 4: Le système LJ de Gentzen



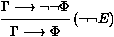
Et la sémantique de Kripke de la logique intuitionniste est donnée par un cadre (W,£), où £ est un ordre (comme pour S4), un domaine non vide D, une interprétation I des symboles de fonction et de prédicats (où I(P), pour chaque prédicat P d'arité m, est une fonction de Dm vers P W et non plus B), et où pour toute affectation r :
Figure 4: Le système LJ de Gentzen
Le cas de la logique linéaire est encore plus frappant. Alors que l'on connait plusieurs sémantiques de la logique linéaire du premier ordre, aucune sémantique n'a été prouvée complète---du moins, aucune sémantique plus simple que le système de preuves. La plupart des résultats en logique linéaire (la cohérence, notamment) n'ont pu être déduits que par l'élimination des coupures et les propriétés des preuves par séquents sans coupure.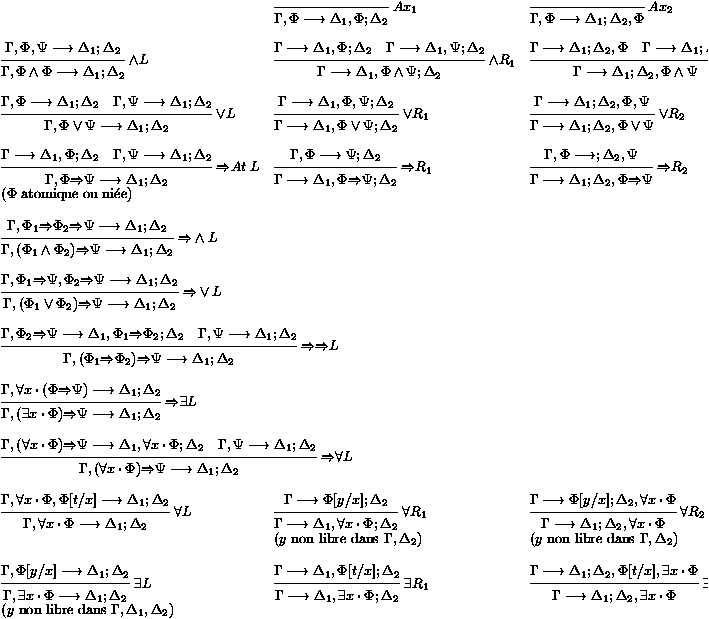
Figure 5: Le système de Miglioli, Moscato et Ornaghi
| R f z 0 ® z |
| R f z (s n) ® f z n (R f z n) |
| " P |
|
· | P(0)Ù (" x |
|
· P(x)Þ P(s(x)))Þ | " x |
|
· P(x) |
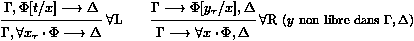
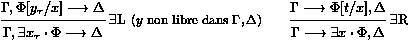
| ¬ $ F |
|
· | " P |
|
· | $ x |
|
· | " y |
|
· FxyÛ Py |
| " P |
|
· | (" x |
|
· | $ y |
|
· Pxy) Þ | ($ f |
|
· | " x |
|
· Px(fx)) |
| " P |
|
· | P($ x |
|
·F(x)) |
| $ x |
|
· F(x) |
| ¬$ x |
|
· F(x) |
| " F |
|
· | " G |
|
· (FÛ G)Û F= G |


