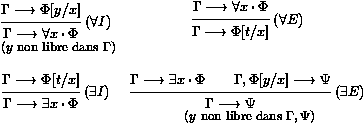
Figure 1: Déduction naturelle en forme de séquents : règles des quantificateurs



La logique classique du premier ordre a aussi des systèmes de déduction naturelle. Par exemple, nous pouvons ajouter les règles de la figure 1 à celles du système ND du chapitre sur la logique propositionnelle classique.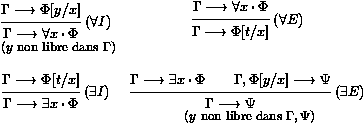
Figure 1: Déduction naturelle en forme de séquents : règles des quantificateurs
Dans le but d'analyser la structure des preuves, nous serons davantage intéressés par le système LK de Gentzen (cf. figure 2). C'est une extension du système LK0 du chapitre sur la logique propositionnelle classique, auquel nous avons ajouté les règles "L, "R, $L, $R sur les quantifications.
Figure 2: Le système LK de Gentzen


