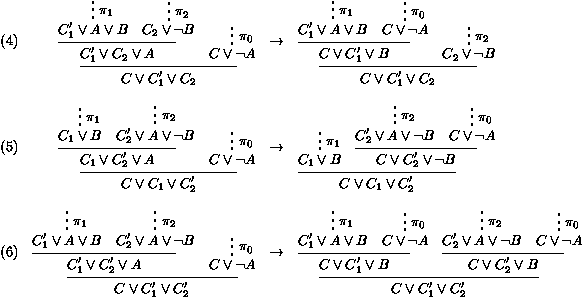|
|
| (1) |
fA (t0, fB (t1, t2)) |
® |
fB (fA (t0, t1), t2) |
| (2) |
fA (t0, fB (t1, t2)) |
® |
fB (t1, fA (t0, t2)) |
| (3) |
fA (t0, fB (t1, t2)) |
® |
fB (fA (t0, t1), fA (t0, t2)) |
| (4) |
fA (fB (t1, t2), t0) |
® |
fB (fA (t1, t0), t2) |
| (5) |
fA (fB (t1, t2), t0) |
® |
fB (t1, fA (t2, t0)) |
| (6) |
fA (fB (t1, t2), t0) |
® |
fB (fA (t1, t0), fA (t2, t0)) |
|
|
ü
ï
ï
ï
ý
ï
ï
ï
þ |
(A > B)
|