

1 Résolution et preuves à base de coupures
Rappelons qu'une clause ¬ A1 Ú ¬ A2 Ú ... Ú ¬
Am Ú B1 Ú B2 Ú ... Ú Bn, où les Ai et les
Bj sont atomiques, n'est qu'une notation commode pour le séquent
atomique:
A1, A2, ..., Am ¾® B1, B2, ..., Bn
La règle de résolution :
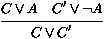
n'est alors rien d'autre que la règle de coupure Cut de LK0,
restreinte aux séquents atomiques :
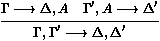
Soit S un ensemble de clauses, et nommons LK0 + S le système
logique obtenue en ajoutant aux règles de LK0 les règles :
pour toute clause G ¾® D dans S.
Toute dérivation par résolution à partir de S est ainsi une
preuve d'un certain séquent dans LK0 + S, et toute
réfutation par résolution est une preuve de la clause vide  ,
c'est-à-dire du séquent vide ¾® dans LK0 + S.
,
c'est-à-dire du séquent vide ¾® dans LK0 + S.
Mais il s'agit d'une preuve d'un format très spécial : la seule
règle de LK0 qu'elle utilise est la coupure Cut. Ceci est
étonnant, parce que c'est en quelque sorte un résultat inverse de
l'élimination des coupures (qui dit que la seule règle inutile en
LK0 serait justement Cut).
On peut en fait montrer la complétude de la résolution en
effectuant les étapes suivantes (consulter la fin du chapitre
``Résolution au premier ordre'' pour plus de détails). Soit F
une formule valide, S une forme clausale de ¬ F (qui est donc
insatisfiable), on souhaite montrer que l'on peut déduire le
séquent vide ¾® à partir de S en utilisant juste la
règle de coupure. Pour ceci :
- Comme S est insatisfiable, S ¾® est prouvable dans
LK0 par la complétude de LK0; d'autre part, ¾®
S est trivialement prouvable dans LK0 + S (pas dans
LK0, évidemment). En utilisant une coupure, on en déduit
que le séquent vide est dérivable dans LK0 + S.
- On applique maintenant les mouvements d'élimination des
coupures (cf. tronc commun, ou bien le chapitre ``Logique classique
du premier ordre''). Ceci fait remonter les coupures le plus haut
possible, et termine. On se retrouve alors avec une preuve de la
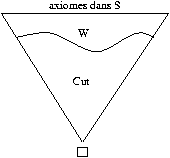
forme :
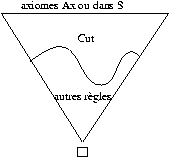 avec tous les axiomes de la forme Ax ou dans S en haut, des
coupures en dessous et toutes les autres règles encore en-dessous.
(Toutes les règles logiques, c'est-à-dire portant sur les
connecteurs logiques, ont en effet nécessairement disparu, parce
que les clauses de S sont des séquents atomiques.)
avec tous les axiomes de la forme Ax ou dans S en haut, des
coupures en dessous et toutes les autres règles encore en-dessous.
(Toutes les règles logiques, c'est-à-dire portant sur les
connecteurs logiques, ont en effet nécessairement disparu, parce
que les clauses de S sont des séquents atomiques.)
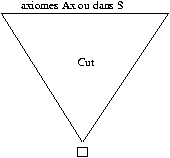
Mais la conclusion étant le séquent vide, la dernière règle
appliquée ne peut être qu'une coupure ou bien un séquent de
S (si la clause vide est dans S). Dans tous les cas, il n'y a
pas d'autre règle que Cut appliquée dans la partie
basse de la preuve, et la preuve est donc de la forme :
- Il ne reste plus qu'à montrer qu'on n'a jamais besoin de la
règle Ax en haut de la preuve. Or aucune instance de Ax ne
peut être la conclusion (clause vide) de la preuve, donc toute
instance de Ax est forcément une prémisse de Cut. On
transforme les cas où la formule axiome (celle qui est la même
de chaque côté du séquent) n'est pas la formule de coupure :
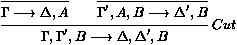
en des instances de Ax (et symétriquement si A est à gauche
du séquent de gauche). Et l'on transforme les cas où la formule
axiome (celle qui est la même de chaque côté du séquent) est
la formule de coupure :
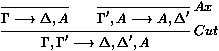
en :
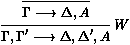
(et symétriquement si A est à gauche du séquent de gauche),
où W est une règle d'affaiblissement que l'on ajoute au
calcul. Comme le processus termine, on obtient une preuve
n'utilisant que les règles Cut, W, et les axiomes de S, de :
- On observe maintenant que l'on peut permuter W et Cut de
sorte à faire descendre les instances de W dans la preuve. Les
instances de W qui introduisent une formule de coupure absorbent
la coupure qui est en-dessous, par exemple :
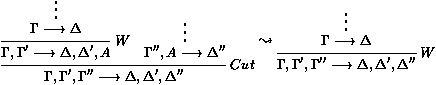
Et les instances de W qui n'introduisent pas la formule de coupure
permutent avec la coupure qui est en-dessous :
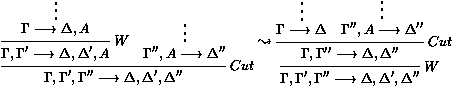
Il est facile de voir que le processus termine, et on aboutit à
une preuve n'utilisant que Cut, W et les axiomes de S de la
forme :
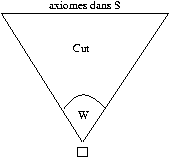
Mais les seules instances de W qui permettent de déduire le
séquent vide (en bas) sont des instances de la forme:
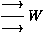
On peut donc toutes les supprimer, et il reste une preuve de la
forme :
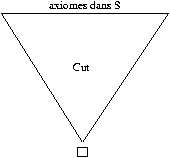
ce qui était la forme souhaitée.
On a ainsi prouvé de façon essentiellement syntaxique (modulo la
preuve de complétude de LK0) que la résolution était une
méthode complète de preuve.
Il y a cependant quelques détails à règler. Dans l'étape 1,
par exemple, on a utilisé S de façon ambiguë soit comme une
formule, soit comme un ensemble de séquents. Il faut être plus
précis : S est une disjonction de conjonctions Di, 1£ i£
n, où Di est la formule Li1 Ú ... Ú Lini, les
Lij étant des littéraux. Soit Ci la clause (le séquent)
que l'on a aussi décidé de noter Li1 Ú ... Ú
Lini. Ce n'est pas S ¾® qui est prouvable, mais D1,
..., Dn ¾®; d'autre part, Di est clairement prouvable
à partir de LK0 + S (partir de Ci), pour tout i : on en
conclut que ¾® est prouvable en LK0 + S, en utilisant
Cut n fois.


 avec tous les axiomes de la forme Ax ou dans S en haut, des
coupures en dessous et toutes les autres règles encore en-dessous.
(Toutes les règles logiques, c'est-à-dire portant sur les
connecteurs logiques, ont en effet nécessairement disparu, parce
que les clauses de S sont des séquents atomiques.)
avec tous les axiomes de la forme Ax ou dans S en haut, des
coupures en dessous et toutes les autres règles encore en-dessous.
(Toutes les règles logiques, c'est-à-dire portant sur les
connecteurs logiques, ont en effet nécessairement disparu, parce
que les clauses de S sont des séquents atomiques.)
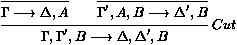
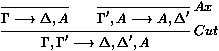
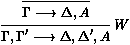

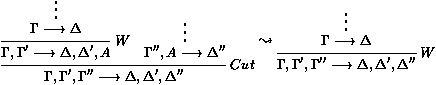
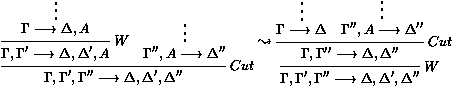




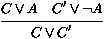
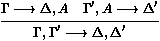
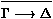
 ,
c'est-à-dire du séquent vide ¾® dans LK0 + S.
,
c'est-à-dire du séquent vide ¾® dans LK0 + S.