CMC Tool
Compositional Model Checking for Real-Time Systems
Compositional Model Checking
The major obstacle for the timed model-checking approach is the state
explosion problem due to the parallel composition (as in the untimed
case) and due to the time encoding. Several heuristics have been
proposed to overcome this problem: symbolic model-checking, on-the-fly
techniques, compact data-structures for time constraints. Given a
network S = (A1 | ... | An) and a
formula F , another possibility consists
in using a compositional approach to avoid the construction of the
product automaton corresponding to S = (A1 |
... | An) : the idea is to remove the component A1 from S and
to encode its pertinent behavior (w.r.t. F
) into a new formula F /A1 which
holds for S'=(A2 | ... | An) iff F holds for
S . Now repeating this operation with
other components leads to the problem of establishing that nil (a process which performs no action at
all) satisfies the last formula (
F/A1.../An). The tool CMC
implements this compositional model-checking. The theoretical basis of
CMC can be found in the paper
CMC: a tool for Compositional
Model-Checking of Real-Time Systems .
Extension to Linear Hybrid Systems
An extension to linear hybrid system has been proposed in
Model-checking for hybrid systems by quotienting and
constraints solving . This provided: Hybrid CMC
(HCMC). An implementation has been done in HCMC (Hybrid and
Compositional Model Checking) for stopwatch automata. The DBM are used
to overapproximate the set of configurations.
HCMC and Timed Control
In a recent paper (a research report "Modal Logics for Timed Control"
is available
here ), the method has been used in order to solve timed
control problems. The idea is to encode the existence of timed
controllers for a system as a timed modal logic formula to be checked
over the system.
An example of verification with CMC
We present a classical example: the train
crossing. This allows us to present the way of using CMC.
We consider a system composed by several trains , a gate and a
controller.
Every automaton is described as in the figure below.
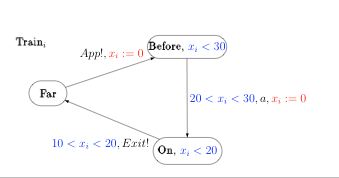
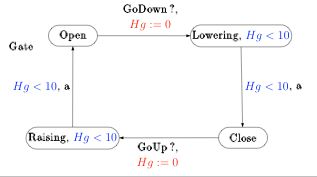

In CMC, the synchronization of the automata is given explicitly in a
table.
The following file contains the full description of the system:
Tsystem
Verifying this system consists in deciding properties like:
- P1 :
When a train is on the crossing, the gate is down.
- P2 :
When an Exit signal is sent by a train, the gate is open in less than
70 t.u. unless another train is approaching or committed in the crossing.
- P3 :
When a train may perform an App or Exit signal, it can be received by
the controller.
These properties can easily be expressed with Lnu -- a timed modal
logic -- handled by CMC.
The following file contains all these properties:
Tprop
Now the verification procedure can be called by typing:
Verify(F1,S,T); and
Verify(F1,S,T); and
Verify(F1,S,T);
An example of timed control
Now the aim is: given the description of the trains and the gate,
does there exist a controller (which outputs signals GoUp and GoDown
) in order to satisfy the following properties:
- P1 :
When a train is on the crossing, the gate is down.
- P2 :
When an Exit signal is sent by a train, the gate is open in less than
50 t.u. unless another train is approaching or committed in the crossing.
We look for a dense-time control: the controller can
prevent time elapsing and force a controllable action to happen at any
point in time. We just require that there are at least D
time units between two controllable actions.
Let C be the self-loop automaton
generating controllable actions s.t. at least D time units separate
these actions. We can then reduce the existence of a controller to a
model checking problem for (Train | Train |
Gate | C ) and the following formula:
Note that the modalities of Lnu are not sufficient to express dense
time control, and we need to use the modality
[@) (its semantics is defined in the research report mentioned
above). The formula X1 defined as follows expresses the existence of a
dense-time controller for the train crossing:
X1 = (*:ON => gate:CLOSE) ^ [App] X1 ^ [i] X1 ^
[Exit] (z in X2) ^ X1 [@) ( < ac > X1) ;
X2 = (gate:OPEN ^ X1) v ((*:ON => gate:CLOSE) ^ z < 50 ^
[Exit] (z in X2) ^ [i] X2 ^ [App] X1 ^ X2 [@) ( < ac > X2))
Indeed the formula holds for (Train | Train |
Gate | C ) : there exists a controller for the system
w.r.t. the properties P1 and P2. Note that such a controller would be
more efficient than the one presented in the previous section because
it opens the gate sooner after the reception of an Exit signal.
Note that this formula ensures the existence of a controller, it does
not provide it (see the research report for a discussion about this
point).
The file of this example is available
here
Simple example
The following example allows us to illustrate the different kinds of
controller we can consider.
Consider the following automaton:
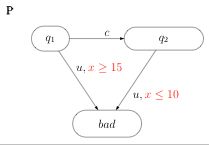
The aim is to avoid the state "bad". Clearly there is a strategy for
this. It is sufficient to let time elapse during T time units with 10
< T < 15 and then perform the controllable transition c.
The existence of a dense-time controller is done by using a selfloop
automaton performing c actions separated by at least D t.u. And we
can verify the following formula over the system:
X1 = - P:BAD ^ [a] X1 ^ X1 [@) (- P:BAD ^ [a] X1 ^ < c > X1)
This allows us to show that there exists a dense time controller for D = 8.
Sampling control
In this case we look for a discrete controller: it can only react at
dates which are multiples of some fixed rate D. In this case, we can
use a standard Lnu formula to state the existence of a sampling
controller:
X1 = - P:BAD ^ [a] X1 ^ ([c] ff v < c > X1) ^ [@] X1
In this case the power of the controller for the time elapsing is
fixed in the self-loop automaton where the controllable actions are
performed exactly every D t.u. Note that we add an dummy action eps in
case where no active controllable action has to be performed at time
D.
For the sampling control, we can show that no controller exist for
D=8, but it is possible when D=3 for example. Clearly dense-time
control is more general than sampling control.
Here the files for these examples:
dense time and
sampling
Download
The tool HCMC is available. It is written in C++, it uses bison and flex.
It works on Linux and MacOs X:
HCMC tool
fl at lsv.ens-cachan.fr





