Optimal Strategies in Priced Timed Game Automata

Authors: Patricia Bouyer, Franck Cassez, Emmanuel Fleury, Kim G. Larsen

Abstract

Priced timed (game) automata extends timed (game) automata with costs on both locations and transitions. In this paper we focus on reachability games for priced timed game automata and prove that the optimal cost for winning such a game is computable under conditions concerning the non-zenoness of cost. Under stronger conditions (strictness of constraints) we prove in addition that it is decidable whether there is an optimal strategy in which case an optimal strategy can be computed. Our results extend previous decidability result which require the underlying game automata to be acyclic. Finally, our results are encoded in a first prototype in HyTech which is applied on a small case-study.

The paper

The theoretical part of this work has been submitted to CONCUR'04 and the algorithm and implementation have been submitted to GDV'04. You can download the pdf version of CONCUR submission as well as the pdf version of the GDV submission. These submitted papers contain no proofs, they can be found in the BRICS Research Report.

Priced Timed Games Automata can generate non-zones polyhedra

We first noticed that optimal strategies for PTGA (Priced Timed Game Automata) do not follow zones, against what is usually the case for timed automata. A simple such example is drawn below. The optimal cost for this PTGA is not an integer, but is a rational number, namely 14+1/3. The optimal strategy is represented on the diagrams on the right.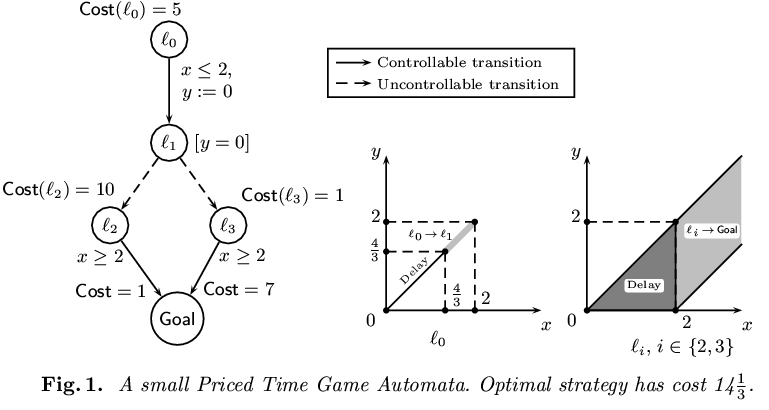

You can download the HyTech file.

The mobile phone example

The model of the mobile connection is the following: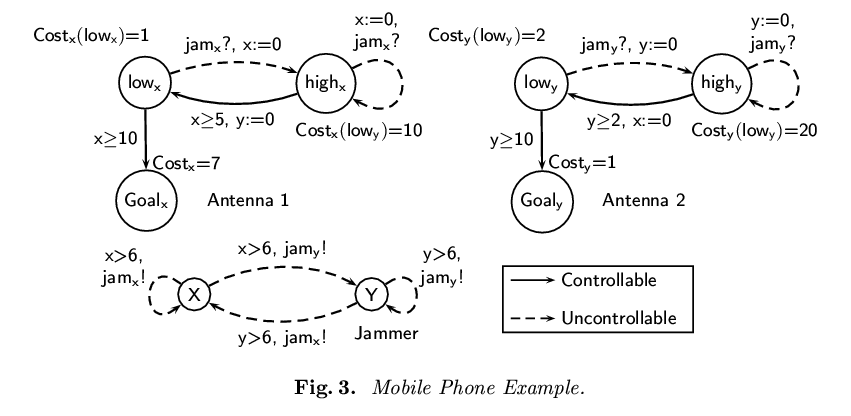

The strategy that we have extracted using HyTech can be described by the following diagrams:

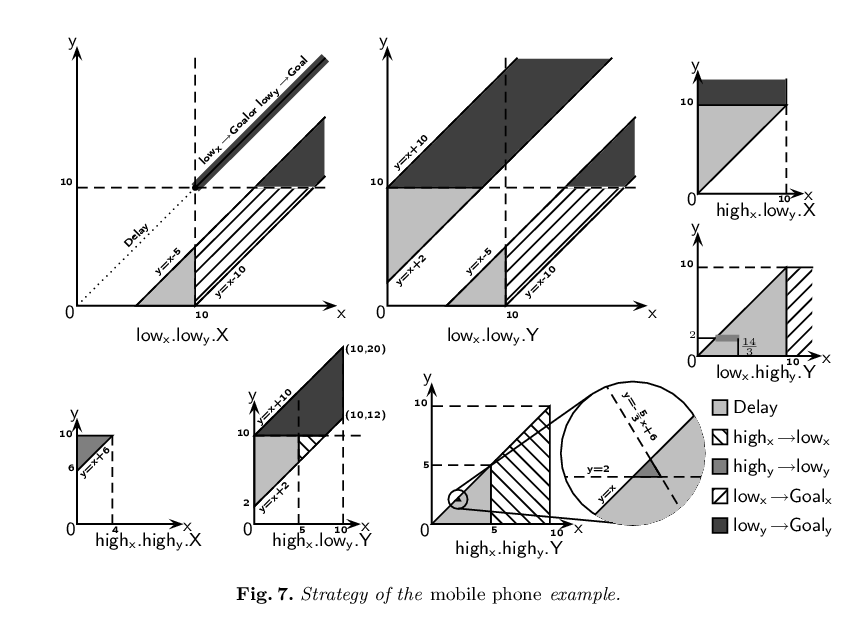
HyTech sources of the mobile phone example

You can download the HyTech file with comments.

Dernières modifications effectuées le 22 novembre 2006 par Patricia Bouyer.